Maximum And Minimum Values Of Trigonometric Functions Trigonometry

Maximum And Minimum Values In Trigonometry For Ssc Exams You can yourself derive the maximum and minimum values of six trigonometric functions from the trigonometric value table for specific angles. maximum and minimum values of $\sin \theta$ and $\cos \theta$ from the table it is clearly seen that maximum and minimum values of both $\sin \theta$ and $\cos \theta$ are $1$ and $ 1$. The entire article has a better understanding of the theoretical concepts of trigonometry and polynomials. it has also answered queries like how to find the maximum and minimum values of trigonometric functions. it also finds out the maximum and minimum value of the quadratic equation formula.

Trigonometry Maximum And Minimum Values Part 1 Ap Maths Youtube However, outside this interval, the minimum value of secant and cosecant is 1 and the maximum value is 1. for a more complex trigonometric expression, you can use calculus (specifically, the first derivative test) to find the maximum and minimum values. the first derivative of a function gives you the slope of the function at any point. In graphing trigonometric functions, we typically use radian measure along the x axis, so the graph would generally look like this: the graph of the standard sine function begins at the zero point, then rises to the maximum value of 1 between 0 and 7 3 radians. it then decreases back to 0 at. So, the minimum value of the trigonometric function a sin x b cos x is − a 2 b 2 and the maximum value is a 2 b 2. we know a ⋅ m. ≥ g. m. sin 2 x csc 2 x 2 ≥ (sin 2 x ⋅ csc 2 x) 1 2. sin 2 x csc 2 x ≥ 2. hence, the answer is option 3. Using a.m ≥ g.m logic for tan 2 θ cot 2 θ we get , = 1 2 sec 2 θ cosec 2 θ. changing into sin and cos values. ( because we know maximum and minimum values of sin θ, cos θ :p and by using simple identities we can convert all trigonometric functions into equation with sine and cosine.).
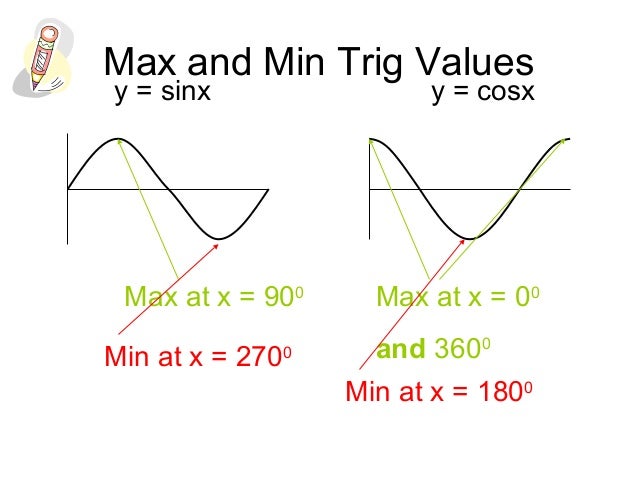
Max And Min Trig Values So, the minimum value of the trigonometric function a sin x b cos x is − a 2 b 2 and the maximum value is a 2 b 2. we know a ⋅ m. ≥ g. m. sin 2 x csc 2 x 2 ≥ (sin 2 x ⋅ csc 2 x) 1 2. sin 2 x csc 2 x ≥ 2. hence, the answer is option 3. Using a.m ≥ g.m logic for tan 2 θ cot 2 θ we get , = 1 2 sec 2 θ cosec 2 θ. changing into sin and cos values. ( because we know maximum and minimum values of sin θ, cos θ :p and by using simple identities we can convert all trigonometric functions into equation with sine and cosine.). The maximum and minimum values are also helpful in determining where the function is increasing or decreasing. in the previous example: the function is increasing between x = −2 x = − 2 and x = −1, x = − 1, then again from x = 3 x = 3 to x = 4. x = 4. so we would say that the intervals in which the function is increasing are −2 ≤ x. The maximum and minimum values of a trigonometric expression can be determined using the properties of trigonometric functions. here are some basic rules: 1. the maximum and minimum values of the sine and cosine functions are 1 and 1 respectively. this is because the range of these functions is @$\begin{align*}[ 1, 1].\end{align*}@$.

Maximum And Minimum Trigonometric Functions Range Ssc Cgs Test Best The maximum and minimum values are also helpful in determining where the function is increasing or decreasing. in the previous example: the function is increasing between x = −2 x = − 2 and x = −1, x = − 1, then again from x = 3 x = 3 to x = 4. x = 4. so we would say that the intervals in which the function is increasing are −2 ≤ x. The maximum and minimum values of a trigonometric expression can be determined using the properties of trigonometric functions. here are some basic rules: 1. the maximum and minimum values of the sine and cosine functions are 1 and 1 respectively. this is because the range of these functions is @$\begin{align*}[ 1, 1].\end{align*}@$.

Maximum And Minimum Value Of Trigonometric Identities Short Trick

How To Find Maximum And Minimum Value In Trigonometry Minimum Maximum

Comments are closed.