Midpoint Theorem вђ Proof Formula Examples And Diagrams
Midpoint Theorem Proof Formula Examples And Diagrams Thus, e is the midpoint of ac, which proves the converse of the midpoint theorem. formula. the midpoint formula helps to find the midpoint between the two given points. if m (x 1, y 1) and n (x 2, y 2) are the coordinates of the two given endpoints of a line segment, then the mid point (x, y) formula will be given by. The example is given below to understand the midpoint theorem. example: in triangle abc, the midpoints of bc, ca, and ab are d, e, and f, respectively. find the value of ef, if the value of bc = 14 cm. solution: given: bc = 14 cm. if f is the midpoint of ab and e is the midpoint of ac, then using the midpoint theorem:.
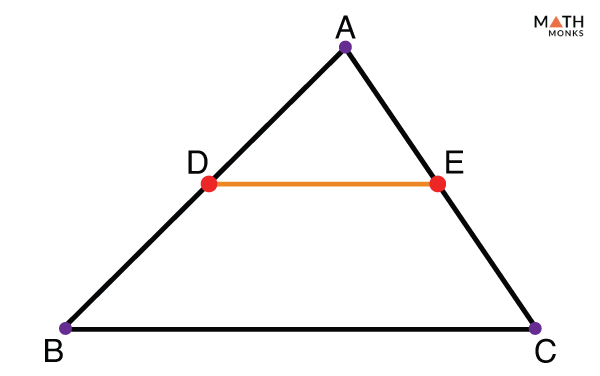
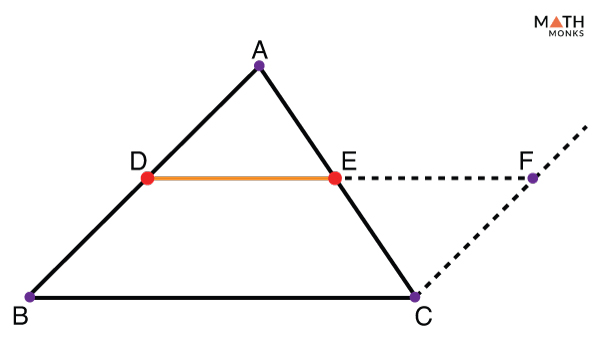
Midpoint Theorem Proof Formula Examples And Diagrams Statement: the midpoint theorem states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the third side. i.e., in a Δabc, if d and e are the midpoints of ab and ac respectively, then de || bc and de = ½ bc. proof of midpoint theorem. now, let us prove the midpoint. The midpoint theorem highlights how the midpoints of the triangle relate to each other. it also defines how the midsegment formed by the midpoints relates to the third side of the triangle. in this article, we’ll break down the conditions needed to utilize the midpoint theorem. we’ll break down the theorem, show the proof behind it, and. So, de:ef = 1:1 (as they are equal) example 2: in the figure given below l, m and n are mid points of side pq, qr, and pr respectively of triangle pqr. if pq = 8cm, qr = 9cm and pr = 6cm. find the perimeter of the triangle formed by joining l, m, and n. solution: as l and n are mid points. by mid point theorem. The midpoint formula is used to identify the coordinates of the midpoint of the line segment. this formula used for the midpoint theorem is familiar to high school students. the point that is equidistant from two points, a (x 1, y 1) and b (x 2, y 2), on a line segment, is known as the midpoint.
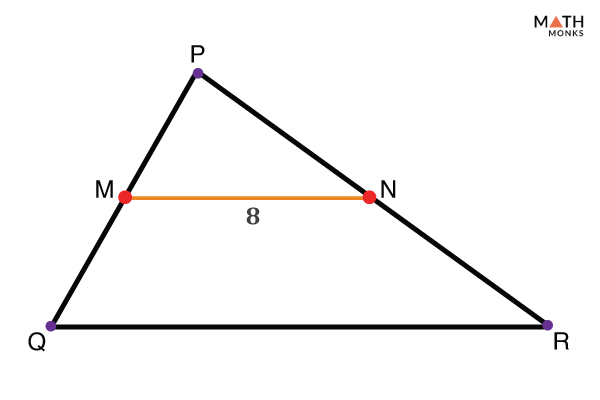
Midpoint Theorem Proof Formula Examples And Diagrams So, de:ef = 1:1 (as they are equal) example 2: in the figure given below l, m and n are mid points of side pq, qr, and pr respectively of triangle pqr. if pq = 8cm, qr = 9cm and pr = 6cm. find the perimeter of the triangle formed by joining l, m, and n. solution: as l and n are mid points. by mid point theorem. The midpoint formula is used to identify the coordinates of the midpoint of the line segment. this formula used for the midpoint theorem is familiar to high school students. the point that is equidistant from two points, a (x 1, y 1) and b (x 2, y 2), on a line segment, is known as the midpoint. The midpoint theorem is one of the important theorems in the concept of geometry. the midpoint theorem deals with the properties of triangles. students can learn about the definition, statement, formula, proof of the midpoint theorem, and examples to find the coordinates of the defined points. related articles: similar triangles; congruency of. According to the mid point theorem, the line joining the mid points of two sides of a triangle is parallel to the third side of the triangle. points \ (c\) and \ (a\) are given on the lines \ (bd\) and \ (be\). study the triangle carefully, then identify and name the parallel lines.

Mid Point Theorem Statement Proof Formula And Example The midpoint theorem is one of the important theorems in the concept of geometry. the midpoint theorem deals with the properties of triangles. students can learn about the definition, statement, formula, proof of the midpoint theorem, and examples to find the coordinates of the defined points. related articles: similar triangles; congruency of. According to the mid point theorem, the line joining the mid points of two sides of a triangle is parallel to the third side of the triangle. points \ (c\) and \ (a\) are given on the lines \ (bd\) and \ (be\). study the triangle carefully, then identify and name the parallel lines.

Comments are closed.