Oscillations On A Mechanically Coupled Bar Pendulum Forced

Oscillations On A Mechanically Coupled Bar Pendulum Forced Chapter 13coupled oscillatorssome oscillations are fairly simple, like the small amplitude swinging of a pendulum, and can be modeled by a single mass on t. e end of a hooke's law spring. others are more complex, but can still be modeled by two or more. asses and two or more springs. examples include compound mechan ical systems, oscillating. Armed with this idea of normal modes, let's take another shot at the system of coupled oscillators shown in figure 8.4.3. we have our two differential equations that include x1 and x2 in equation 8.4.7. now we are looking for a pair of new coordinates, q1 and q2, that express the motions of the normal modes.

7 Forced Oscillations Of Coupled Pendulums Modelling The Fano Mites 2017–physics iii. lecture 06: coupled oscillations. in these notes we consider the dynamics of oscillating systems coupled together. to fully describe such systems we introduce the linear algebra concepts of eigenvectors and eigenvalues. we end by considering what the dynamics might look like if we considered an arbitrarily large system. Using newton’s second law (f net = ma f → n e t = m a →), we can analyze the motion of the mass. the resulting equation is similar to the force equation for the damped harmonic oscillator, with the addition of the driving force: −kx − bdx dt f0 sin(ωt) = md2x dt2. (15.7.1) (15.7.1) − k x − b d x d t f 0 sin. ⁡. Simple harmonic motion. you should be able to draw a free body diagram and express the force in terms of the displacement. use newton’s law: = or =. write it in standard form: . solutions are of the = form: = cos. = 0 −. sin. you must be able to use the initial conditions to solve for the constants of integration. In figure \(\pageindex{1b}\), it is the frequency of the envelope of the amplitude of the oscillation of either of the pendulums. all these phenomena will return in the next section, in the study of waves, which travel in a medium in which many oscillators are coupled to one another (figure \(\pageindex{2}\)).

Solution Forced Oscillation Of Two Pendula System Studypool Simple harmonic motion. you should be able to draw a free body diagram and express the force in terms of the displacement. use newton’s law: = or =. write it in standard form: . solutions are of the = form: = cos. = 0 −. sin. you must be able to use the initial conditions to solve for the constants of integration. In figure \(\pageindex{1b}\), it is the frequency of the envelope of the amplitude of the oscillation of either of the pendulums. all these phenomena will return in the next section, in the study of waves, which travel in a medium in which many oscillators are coupled to one another (figure \(\pageindex{2}\)). Also there will be an oscillation at ε= 1 2 (442−339)hz=1.5hz. this oscillation is the enveloping curve over the high frequency (440.5 hz) oscillations figure 3. the red curve is cos 2πν1−ν2 2 t . when hearing beats, the observed frequency is the fre quency of the extrema νbeat =ν1−ν2 which is twice the frequency of this curve . 2.1 the coupled pendulum rather than a single pendulum, now let us consider two pendula which are coupled together by a spring which is connected to the masses at the end of two thin strings. the spring has a spring constant of k and the length, l of each string is the same, as shown in fig. 2.1 unlike the simple pendulum with a single string.

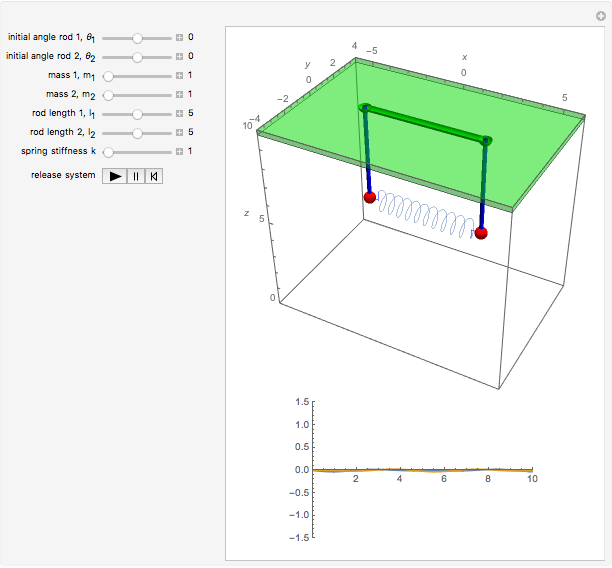
Coupled Pendulum Oscillations Wolfram Demonstrations Project Also there will be an oscillation at ε= 1 2 (442−339)hz=1.5hz. this oscillation is the enveloping curve over the high frequency (440.5 hz) oscillations figure 3. the red curve is cos 2πν1−ν2 2 t . when hearing beats, the observed frequency is the fre quency of the extrema νbeat =ν1−ν2 which is twice the frequency of this curve . 2.1 the coupled pendulum rather than a single pendulum, now let us consider two pendula which are coupled together by a spring which is connected to the masses at the end of two thin strings. the spring has a spring constant of k and the length, l of each string is the same, as shown in fig. 2.1 unlike the simple pendulum with a single string.

Coupled Pendulum Pdf Pendulum Oscillation