Polynomial Functions And Equations Lesson 3 Synthetic Division

Polynomial Functions And Equations Lesson 3 Synthetic Division The remainder theorem. for any polynomial p(x) of degree 1 or higher and any real number k, p(k) is equal to the remainder of the division of p(x) by x − k. algebraically: if p(x) x − k = q(x) r x − k, then p(k) = r. as always, an equality is true “both ways”. in the remainder theorem, we can say that. Synthetic division method. i have to admit, synthetic division is probably the most “fun” method for dividing polynomials. it’s more straightforward than polynomial long division and involves fewer steps to get to the answer. in this lesson, i’ll walk you through five examples that should help you get comfortable with the basic steps.

Synthetic Division Of Polynomials Youtube Because x 3 is a factor of the polynomial, 3 is also a solution to the equation x2 2x – 15 0 and a zero of the polynomial function. check that p(3) 0: p(3) 32 2 3 15 9 6 15 0 every linear factor of the polynomial corresponds to a zero of the polynomial function, and every zero of the polynomial function corresponds to a linear factor. Step 1: write the coefficients of the dividend inside the box and zero of x 2 as the divisor. step 2: bring down the leading coefficient 1 to the bottom row. step 3: multiply 2 by 1 and write the product 2 in the middle row. step 4: add 1 and 2 in the second column and write the sum 1 in the bottom row. For example, suppose the volume of a rectangular solid is given by the polynomial 3 x 4 − 3 x 3 − 33 x 2 54 x. 3 x 4 − 3 x 3 − 33 x 2 54 x. the length of the solid is given by 3 x; 3 x; the width is given by x − 2. x − 2. to find the height of the solid, we can use polynomial division, which is the focus of this section. using. In order to use synthetic division we must be dividing a polynomial by a linear term in the form x−r x − r. if we aren’t then it won’t work. let’s redo the previous problem with synthetic division to see how it works. example 2 use synthetic division to divide 5x3 −x2 6 5 x 3 − x 2 6 by x −4 x − 4. show solution.

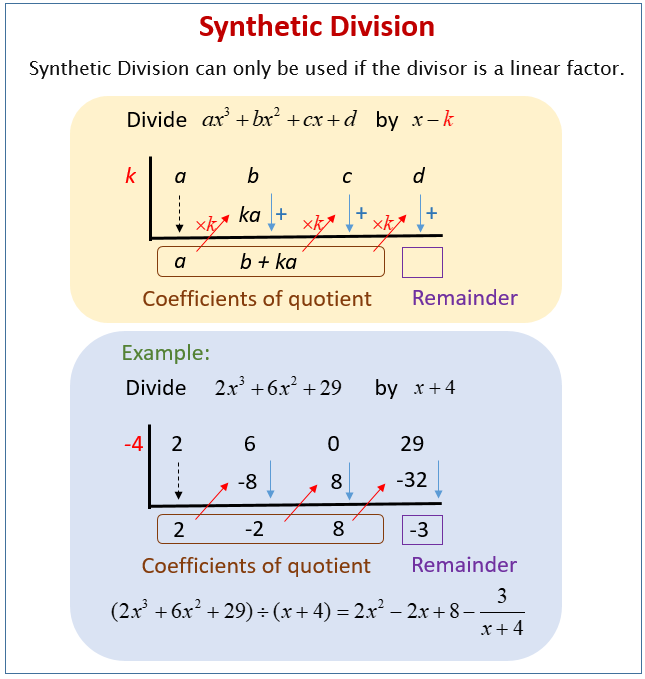
Dividing Polynomials Using Synthetic Division Solutions Examples For example, suppose the volume of a rectangular solid is given by the polynomial 3 x 4 − 3 x 3 − 33 x 2 54 x. 3 x 4 − 3 x 3 − 33 x 2 54 x. the length of the solid is given by 3 x; 3 x; the width is given by x − 2. x − 2. to find the height of the solid, we can use polynomial division, which is the focus of this section. using. In order to use synthetic division we must be dividing a polynomial by a linear term in the form x−r x − r. if we aren’t then it won’t work. let’s redo the previous problem with synthetic division to see how it works. example 2 use synthetic division to divide 5x3 −x2 6 5 x 3 − x 2 6 by x −4 x − 4. show solution. Synthetic division is a shorthand method of dividing polynomials for the special case of dividing by a linear factor whose leading coefficient is 1. to illustrate the process, recall the example at the beginning of the section. divide 2x3 −3x2 4x 5 2 x 3 − 3 x 2 4 x 5 by x 2 x 2 using the long division algorithm. Synthetic division is a shorthand, or shortcut, method of polynomial division in the special case of dividing by a linear factor — and it only works in this case. synthetic division is generally used, however, not for dividing out factors but for finding zeroes (or roots) of polynomials. more about this later.