Ppt Addition Rules For Probability Powerpoint Presentation Free

Ppt Addition Rules Of Probability Powerpoint Presentation Free This document discusses addition rules and complementary events in probability. it provides examples of using the addition rule to calculate the probability of compound events using p (a or b) = p (a) p (b) p (a and b). it also discusses that if events are mutually exclusive, p (a and b) = 0 so the formula simplifies to p (a or b) = p (a. Section 4.2 discusses the addition rule and multiplication rule for finding probabilities of compound events. the addition rule states that the probability of event a or b occurring is equal to the probability of a plus the probability of b minus the probability of both a and b occurring. the multiplication rule is used to find the probability.

Ppt Addition Rules For Probability Powerpoint Presentation Free The box represents the entire sample space and must add up to 1. that means the entire a circle must add up to0.8. the probability that a student fits the event aand b is0.2. that means the entire b circle must add up to0.3. 0.6 0.6 0.2 0.2 0.1 0.1 0.1 0.1. a b = 0.9 answer then find the probability of a or b. Complements, disjoint events, and the addition rule. complements, disjoint events, and the addition rule. presentation 4.3 overview. probability rules. the probability p(a) of any event is always a number between 0 and 1. the probability that you can read this is 1 (since we know for a fact you are reading it right now). 203 views • 7 slides. This document discusses basic concepts of probability, including: the addition rule and multiplication rule for calculating probabilities of compound events. events can be disjoint (mutually exclusive) or not disjoint. the probability of an event occurring or its complement must equal 1. how to calculate the probability of at least one. First fill in where the events overlap. the box represents the entire sample space and. must add up to 1. that means the entire a circle must add up to 0.8. the probability that a student fits the event a. and b is 0.2. that means the entire b circle must add up to. 0.3.

Ppt Addition Rules Of Probability Powerpoint Presentation Free This document discusses basic concepts of probability, including: the addition rule and multiplication rule for calculating probabilities of compound events. events can be disjoint (mutually exclusive) or not disjoint. the probability of an event occurring or its complement must equal 1. how to calculate the probability of at least one. First fill in where the events overlap. the box represents the entire sample space and. must add up to 1. that means the entire a circle must add up to 0.8. the probability that a student fits the event a. and b is 0.2. that means the entire b circle must add up to. 0.3. Section 4.3 the addition rules for probability. section 4.3 the addition rules for probability. objectives: determine if two or more simple events are mutually exclusive or not find the probability of compound events, using the addition rule(s). recall: compound event: any event containing two or more simple events key word: or. 416 views • 8. A powerpoint covering probability up to higher gcse level. assumes that the basics have already been covered, but includes: venn diagrams and set notation addition law two way tables frequency trees and probability trees (both with and without replacement) conditional probability using venn diagrams and two way tables.
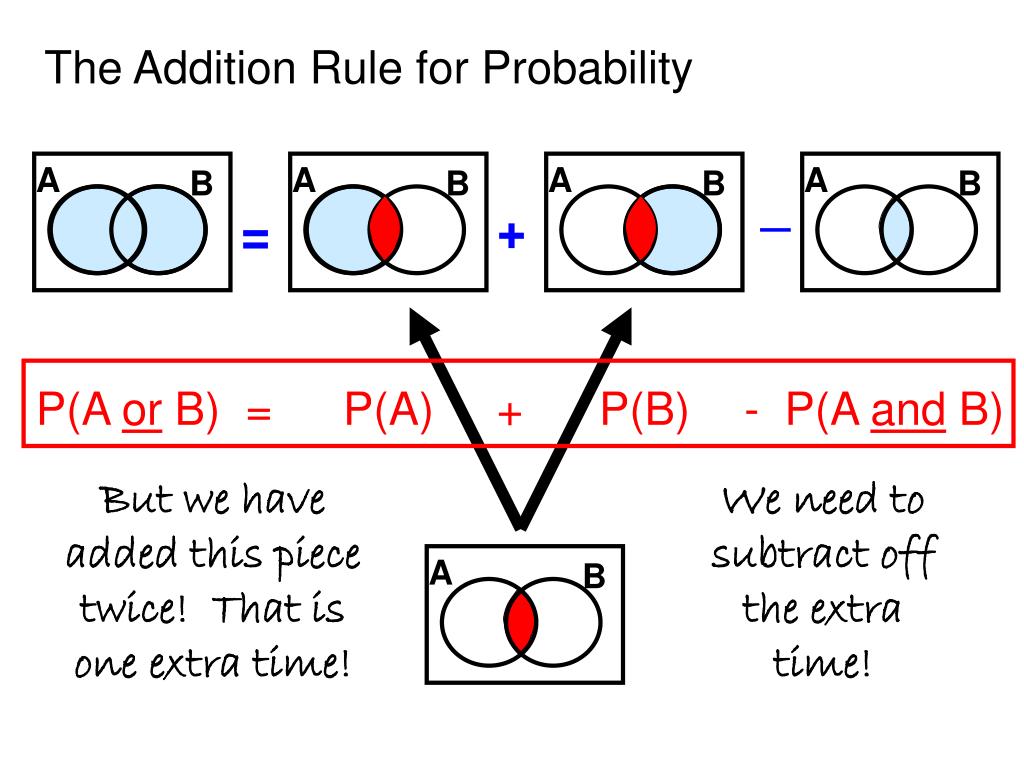
Ppt Addition Rule For Probability Powerpoint Presentation Free Section 4.3 the addition rules for probability. section 4.3 the addition rules for probability. objectives: determine if two or more simple events are mutually exclusive or not find the probability of compound events, using the addition rule(s). recall: compound event: any event containing two or more simple events key word: or. 416 views • 8. A powerpoint covering probability up to higher gcse level. assumes that the basics have already been covered, but includes: venn diagrams and set notation addition law two way tables frequency trees and probability trees (both with and without replacement) conditional probability using venn diagrams and two way tables.

Comments are closed.