Producto Punto De Vectores вђ Clases De Mecгўnica

Producto Punto De Vectores Clases De Mecánica Dot product. el producto punto o producto escalar de dos vectores, por definición, es el resultado de multiplicar los módulos de ambos vectores por el coseno del ángulo que forman. ¡siendo α el ángulo que forman los dos vectores!! ¡cuidado! el resultado del producto punto o producto escalar es un número. no confundir con el producto. El producto punto de los vectores a y b se denota como: a → ⋅ b →. se lee como "a punto b", y está definido como la suma de los productos de las componentes correspondientes de los dos vectores. matemáticamente, el producto punto de vectores en un espacio de “n” dimensiones se expresa de la siguiente manera: a → ⋅ b → = a 1 b.

Producto Punto De 2 Vectores Youtube Sean a →, b → y c → vectores y m un escalar, el producto punto cumple las siguientes propiedades: propiedad conmutativa del producto punto. propiedad conmutativa del producto punto de vectores: a → ⋅ b → = b → ⋅ a →. esta propiedad establece que el producto punto es conmutativo, es decir, no importa el orden en el que se. Podemos calcular el producto punto de dos vectores de esta manera: a · b = | a | × | b | × cos (θ) entonces multiplicamos la longitud de a por la longitud de b, luego multiplicamos por el coseno del ángulo entre a y b. o lo podemos calcular de esta manera: a · b = a x × b x a y × b y. entonces multiplicamos las x, multiplicamos las y. Al igual que la suma y resta de vectores, el producto de punto tiene varias propiedades algebraicas. demostramos tres de estas propiedades y dejamos el resto como ejercicios. propiedades del producto dot. dejar ⇀ u, ⇀ v, y ⇀ w ser vectores, y dejar c ser un escalar. propiedad conmutativa ⇀ u ⋅ ⇀ v = ⇀ v ⋅ ⇀ u. Propiedades del producto dot. el producto punto se define como: u ⋅ v = <u1, u2> ⋅ <v1, v2> = u1v1 u2v2. este procedimiento establece que se multiplican los valores correspondientes y luego se suman los productos resultantes. se puede trabajar con vectores que son más de dos dimensiones de la misma manera.

Producto Punto De Vectores Clases De Mecánica Al igual que la suma y resta de vectores, el producto de punto tiene varias propiedades algebraicas. demostramos tres de estas propiedades y dejamos el resto como ejercicios. propiedades del producto dot. dejar ⇀ u, ⇀ v, y ⇀ w ser vectores, y dejar c ser un escalar. propiedad conmutativa ⇀ u ⋅ ⇀ v = ⇀ v ⋅ ⇀ u. Propiedades del producto dot. el producto punto se define como: u ⋅ v = <u1, u2> ⋅ <v1, v2> = u1v1 u2v2. este procedimiento establece que se multiplican los valores correspondientes y luego se suman los productos resultantes. se puede trabajar con vectores que son más de dos dimensiones de la misma manera. El objetivo de esta clase los vectores en $\mathbb{r}^{n}$ y explorar algunas operaciones entre vectores como la suma y producto por escalar de vectores. también estudiamos el producto punto entre vectores, el concepto de norma de un vector y el ángulo entre vectores. para esta clase puedes encontrar material dividido de la siguiente manera: 1. DefiniciÓn. producto punto. el producto punto de los vectores u = u ₁, u ₂, u ₃ y v = v ₁, v ₂, v ₃ viene dado por la suma de los productos de los componentes. u ∙ v = u₁ v₁ u₂ v₂ u₃ v₃. ♦. tenga en cuenta que si u y v son vectores bidimensionales, calculamos su producto punto de manera similar.
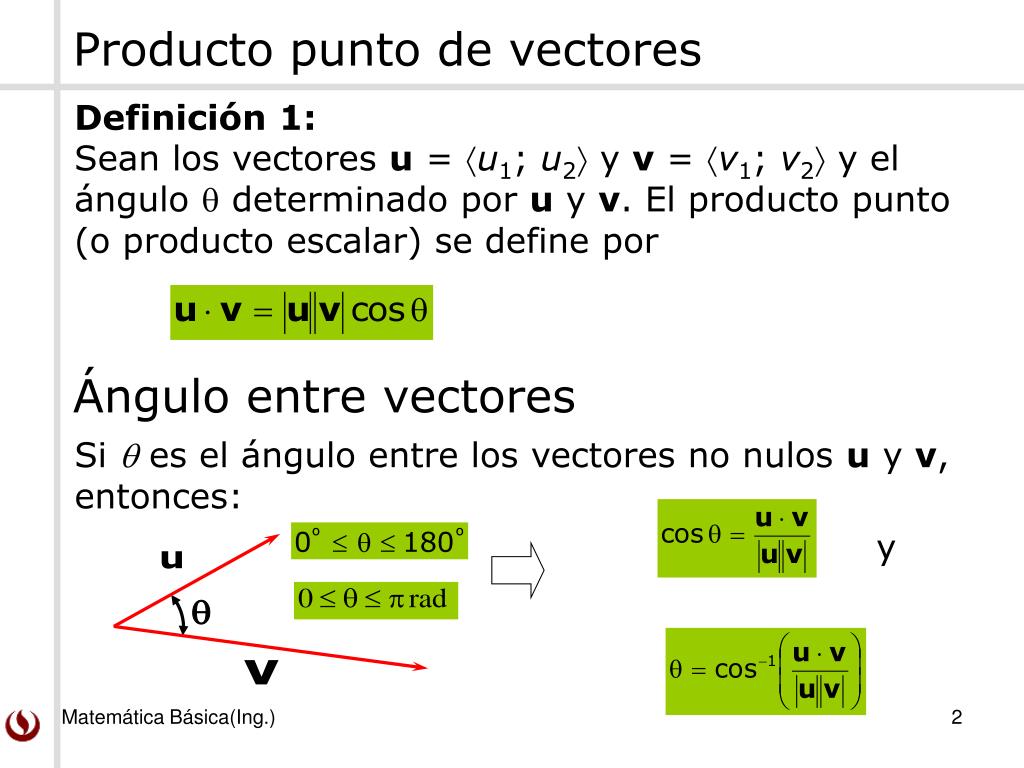
Ppt Producto Punto De Vectores Powerpoint Presentation Free Download El objetivo de esta clase los vectores en $\mathbb{r}^{n}$ y explorar algunas operaciones entre vectores como la suma y producto por escalar de vectores. también estudiamos el producto punto entre vectores, el concepto de norma de un vector y el ángulo entre vectores. para esta clase puedes encontrar material dividido de la siguiente manera: 1. DefiniciÓn. producto punto. el producto punto de los vectores u = u ₁, u ₂, u ₃ y v = v ₁, v ₂, v ₃ viene dado por la suma de los productos de los componentes. u ∙ v = u₁ v₁ u₂ v₂ u₃ v₃. ♦. tenga en cuenta que si u y v son vectores bidimensionales, calculamos su producto punto de manera similar.

Producto Punto De Vectores Clases De Mecánica

Comments are closed.