Producto Vectorial De Vectores

Producto Vectorial De Dos Vectores O Producto Cruz Ejercicios Resueltos Aprende qué es el producto vectorial de dos vectores, cómo se calcula con una fórmula o un determinante, y cómo se determina su dirección y sentido con la regla de la mano derecha o del sacacorchos. también descubre sus propiedades y aplicaciones en geometría y física. Calcular el producto vectorial implica seguir un procedimiento específico, que puede dividirse en pasos para hacerlo más comprensible. a continuación, se presenta un ejemplo práctico de cómo calcular el producto vectorial de dos vectores: identificar los vectores: supongamos que ( mathbf{a} = (3, 2, 1) ) y ( mathbf{b} = (1, 0, 2) ).

Producto Vectorial O Cruz De Vectores En Física Aprende qué es el producto vectorial de dos vectores, cómo se calcula, qué reglas y propiedades tiene, y cómo se representa en el espacio. encuentra también ejercicios resueltos y fórmulas analíticas. En concreto, el vector de fuerza magnética es el producto vectorial f → = ζ u → × b → f → = ζ u → × b → y, por la definición del producto vectorial (vea la figura 2.29), el vector f → f → debe ser perpendicular a ambos vectores u → u → y b → b →. Producto vectorial. el área de un paralelogramo como la magnitud de un producto cruzado. en matemáticas, el producto vectorial de gibbs o producto cruz es una operación binaria entre dos vectores en un espacio tridimensional. el resultado es un vector perpendicular a los vectores que se multiplican, y por lo tanto normal al plano que los. El producto vectorial es muy útil para varios tipos de cálculos, como hallar un vector ortogonal a dos vectores dados, calcular áreas de triángulos y paralelogramos e incluso determinar el volumen de la forma geométrica tridimensional hecha de paralelogramos conocida como paralelepípedo. los siguientes ejemplos ilustran estos cálculos.

Producto Vectorial Youtube Producto vectorial. el área de un paralelogramo como la magnitud de un producto cruzado. en matemáticas, el producto vectorial de gibbs o producto cruz es una operación binaria entre dos vectores en un espacio tridimensional. el resultado es un vector perpendicular a los vectores que se multiplican, y por lo tanto normal al plano que los. El producto vectorial es muy útil para varios tipos de cálculos, como hallar un vector ortogonal a dos vectores dados, calcular áreas de triángulos y paralelogramos e incluso determinar el volumen de la forma geométrica tridimensional hecha de paralelogramos conocida como paralelepípedo. los siguientes ejemplos ilustran estos cálculos. Aprende qué es el producto vectorial de dos vectores, cómo se calcula su magnitud y dirección, y cómo se usa en física y astronomía. explora ejemplos, ejercicios, gráficos y la regla de la mano derecha con hyperphysics. Cuando tenemos las magnitudes de los vectores y el ángulo entre sus direcciones, la magnitud de su producto vectorial es calculado con la siguiente fórmula: \vec {a}\times \vec {b}=ab\sin (\theta) a × b = ab sin(θ) en donde, a a y b b son las magnitudes de \vec {a} a y \vec {b} b respectivamente, y \theta θ es el ángulo entre los vectores.

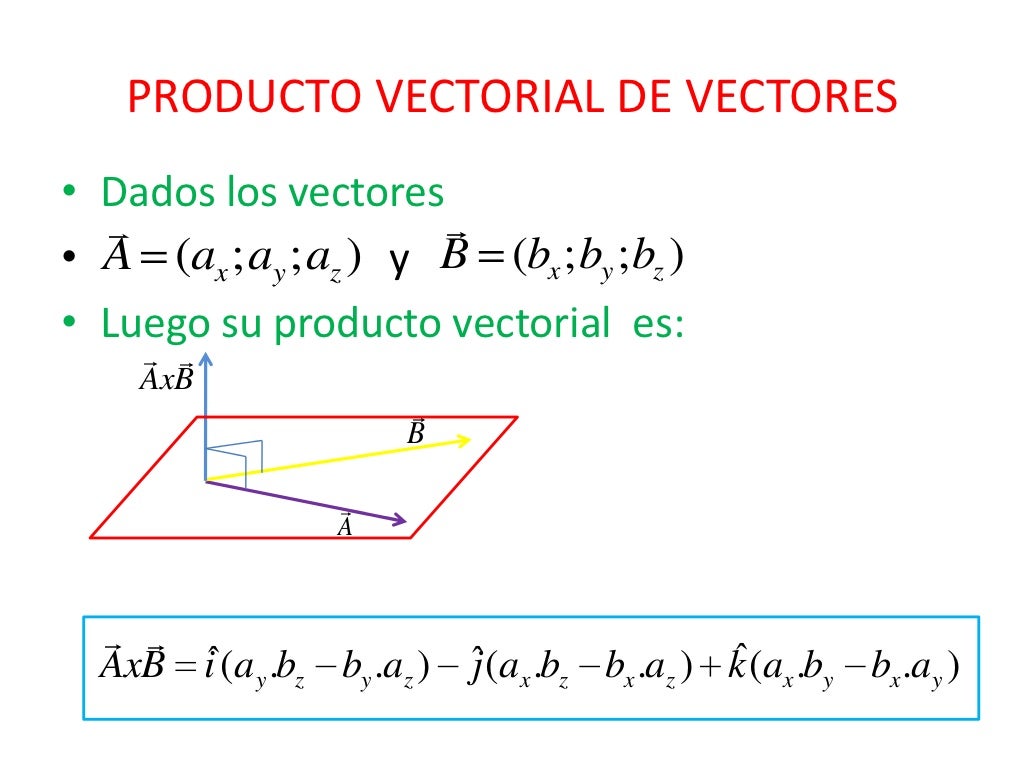
Producto Vectorial De Vectores Aprende qué es el producto vectorial de dos vectores, cómo se calcula su magnitud y dirección, y cómo se usa en física y astronomía. explora ejemplos, ejercicios, gráficos y la regla de la mano derecha con hyperphysics. Cuando tenemos las magnitudes de los vectores y el ángulo entre sus direcciones, la magnitud de su producto vectorial es calculado con la siguiente fórmula: \vec {a}\times \vec {b}=ab\sin (\theta) a × b = ab sin(θ) en donde, a a y b b son las magnitudes de \vec {a} a y \vec {b} b respectivamente, y \theta θ es el ángulo entre los vectores.

Producto Vectorial O Producto Cruz Youtube