Prove That The Area Of The Equilateral Triangle Described On One

By viagraultimate On Nov 9, 2024 Last updated

Area Of An Equilateral Triangle Formula Examples Definition Ex 6.4, 7 (introduction) prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals. concept 1 two equilateral triangle are always similar in ∆ 𝐴𝐵𝐶 𝑎𝑛𝑑 ∆ 𝐷𝐸𝐹 𝐷𝐸 𝐴𝐵=12 6 𝐸𝐹 𝐵𝐶=12. Let’s plug in the value of the area then solve for the side: learn the method for calculating the area of an equilateral triangle using the formula area = (√3 4)s^2, where 's' denotes the side length of the equilateral triangle. keep in mind that all sides of an equilateral triangle are of equal length.

Prove That The Area Of An Equilateral Triangle Described On One Side Of Ncert class 10 maths solutions chapter 6 exercise 6.4 question 7. prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals. Q. prove that the area of an equilateral triangle described on one side of a square is equal to half the area of an equilateral triangle described on one of its diagonals. or, prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides. Examples on area of equilateral triangle. example 1: find the area of an equilateral triangle of side 9 cm. solution: the formula for the area of an equilateral triangle is given as, area = √ (3) 4 × (side) 2. by substituting the value of side length in the above formula, we get, = √ (3) 4 × 9 2. = 35.07 inches 2. So, the area of the equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonals. note in order to solve these types of problems related to the property of triangles first of all remembers all the properties and theorems of the triangle.

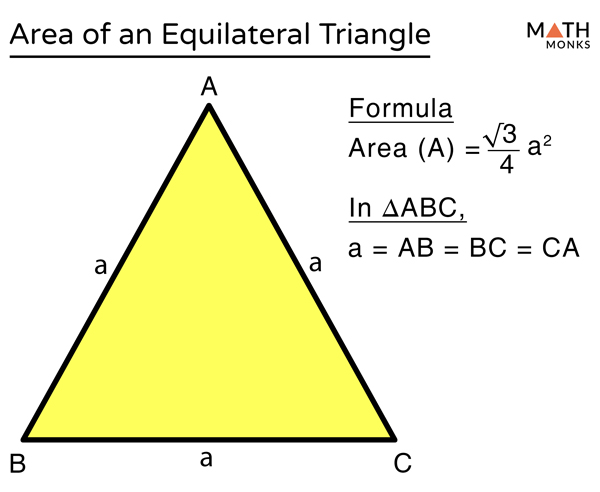
Equilateral Triangle Definition Properties Formulas Examples on area of equilateral triangle. example 1: find the area of an equilateral triangle of side 9 cm. solution: the formula for the area of an equilateral triangle is given as, area = √ (3) 4 × (side) 2. by substituting the value of side length in the above formula, we get, = √ (3) 4 × 9 2. = 35.07 inches 2. So, the area of the equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonals. note in order to solve these types of problems related to the property of triangles first of all remembers all the properties and theorems of the triangle. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals. view solution q 2. Class 10 ll chapter triangles ex : 6.4 ll question no.7 prove that the area of an equilateral triangle described on one side of a square is equal to half th.

Immerse yourself in the fascinating realm of Prove That The Area Of The Equilateral Triangle Described On One through our captivating blog. Whether you're an enthusiast, a professional, or simply curious, our articles cater to all levels of knowledge and provide a holistic understanding of Prove That The Area Of The Equilateral Triangle Described On One. Join us as we dive into the intricate details, share innovative ideas, and showcase the incredible potential that lies within Prove That The Area Of The Equilateral Triangle Described On One.

Prove that the area of the equilateral triangle described on one side of a square is equal to half

Prove that the area of the equilateral triangle described on one side of a square is equal to half Prove that the area of an equilateral triangle described on one side of the square is Prove that area of the equilateral triangle described on side of a square is half the area of .... Prove that the area of an equilateral triangle described on one side of a square is equal to half Prove that the area of an equilateral triangle described on one side of the square is equal to half Prove that the area of an equilateral triangle described on one side of a square is equal - Teachoo Prove that the area of an equilateral triangle described on one side of a square is equal to half Provethat the area of an equilateral triangle described on one side of a square isequal to half ... Find the area under the curve #mathshorts #integralcalculus Prove that the area of the equilateral triangle described on the side of a square is half the ar... Prove that the area of an equilateral triangle described on one side of the square is equal to half class 10 Prove that the area of an equilateral triangle described on one side of a square is equal What is the Area of an Equilateral Triangle? Prove that the area of equilateral triangle describing on one side of a square is half of the area o Q7-Ex6.4-Ncert-Prove that the area of an equilateral triangle described on one side of a square.... Prove that the area of equilateral triangle described on one side of the square is equal to half th prove area of equilateral triangle described on side of square half area of equilateral on diagonal Prove that the area of an equilateral triangle described on one side of a square is equal to hal... Prove that area of an equilateral triangle described on one side of a square is equal to half area Prove that the area of an equilateral triangle described on one side of a square is equal

Conclusion

Delving deeply into the topic, it is unmistakable that this particular content supplies beneficial details related to Prove That The Area Of The Equilateral Triangle Described On One. Throughout the content, the author manifests a wealth of knowledge in the domain. Crucially, the chapter on X stands out as extremely valuable. Whats more, the write-up is exceptional in explaining complex concepts in an accessible manner. What’s more, the commentator imparts case studies that augment the contents usefulness. Another facet that makes this composition outstanding is the detailed examination of numerous aspects related to Prove That The Area Of The Equilateral Triangle Described On One. The scribes systematic manner assures that followers receive a thorough understanding of the subject matter. Thank you for considering this post. If you need further information, feel no hesitation to touch base through the medium of email. I am keen on your messages. In finishing up, if you wish to read more, highlighted below are a collection of related essays that you may find worthwhile:May you find them engaging!