Question 1 A Square Is Inscribed In An Isosceles Right Triangle Have

By viagraultimate On Nov 11, 2024 Last updated

Question 1 A Square Is Inscribed In An Isosceles Right Triangle Have A square of side 1 is inscribed in a right angled triangle so that two sides of the square are along the sides of the triangle and one vertex of the square is on the hypotenuse.if the hypotenuse is 2 √ 6, then the ratio of the other two sides is. In this educational video, we explore the fascinating concept of inscribing a square within an isosceles right triangle. join us as we delve into the mathema.

A Square Is Inscribed In A Right Isosceles Triangle Such That Two Of 4. reflect the triangle across its legs ab a b and bc b c. because ab = bc = 2 a b = b c = 2, the resulting figure is a square. moreover, since the inscribed yellow shape is also a square, it is easy to see that their reflections must form a central square that is congruent, and in fact, the entire figure consists of 9 9 congruent squares. A square of side 1 is inscribed in a right angled triangle so that two sides of the square are along the sides of the triangle and one vertex of the square is on the hypotenuse.if the hypotenuse is 2 √ 6, then the ratio of the other two sides is. Q. nta square with side lengthx is inscribed in a right triangle with sides of length3,4 and5so that one vertex of the square coincides with the right angle vertex of the triangle. a square with side lengthy is inscribed in another right triangle with sides of length3,4 and5 so that one side of the square lies on the hypotenuse of the triangle. Given, a square is inscribed in an isosceles right triangle. the square and the triangle have one angle in common. we have to show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse. consider an isosceles right triangle abc right angled at a. a square def is inscribed in the triangle. given, ∠a = 90°.

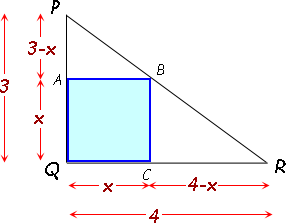
Inscribed Square In A Triangle Math Central Q. nta square with side lengthx is inscribed in a right triangle with sides of length3,4 and5so that one vertex of the square coincides with the right angle vertex of the triangle. a square with side lengthy is inscribed in another right triangle with sides of length3,4 and5 so that one side of the square lies on the hypotenuse of the triangle. Given, a square is inscribed in an isosceles right triangle. the square and the triangle have one angle in common. we have to show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse. consider an isosceles right triangle abc right angled at a. a square def is inscribed in the triangle. given, ∠a = 90°. 1. there is an isosceles triangle with base a = 10 a = 10 and sides b = 13 b = 13. a square is inscribed inside of this triangle such that two of it's vertices are touching base and two of them are touching sides. what is the length of a side of the square? the solution is 60 11 60 11, but i don't know how to arrive at it. geometry. triangles. To find the area of an isosceles right triangle, we use the formula: area = ½ × base × height. in this instance, one of the equal sides is considered the base and the other the height. so, if the two equal sides have a measurement of 4cm, insert the measurements for the base and the height to find the actual area. next, follow these steps:.

24 Bdef Is A Square Formed Inside An Isosceles Right Triangle Abc 1. there is an isosceles triangle with base a = 10 a = 10 and sides b = 13 b = 13. a square is inscribed inside of this triangle such that two of it's vertices are touching base and two of them are touching sides. what is the length of a side of the square? the solution is 60 11 60 11, but i don't know how to arrive at it. geometry. triangles. To find the area of an isosceles right triangle, we use the formula: area = ½ × base × height. in this instance, one of the equal sides is considered the base and the other the height. so, if the two equal sides have a measurement of 4cm, insert the measurements for the base and the height to find the actual area. next, follow these steps:.

Geometry Square Inscribed In An Isosceles Right Triangle

A Square Is Inscribed In An Isosceles Right Angled Triangle So That

Whether you're looking for practical how-to guides, in-depth analyses, or thought-provoking discussions, we are has got you covered. Our diverse range of topics ensures that there's something for everyone, from Question 1 A Square Is Inscribed In An Isosceles Right Triangle Have. We're committed to providing you with valuable information that resonates with your interests.

A square is inscribed in an isosceles right triangle so that the square and the triangle have one...

A square is inscribed in an isosceles right triangle so that the square and the triangle have one... A square is inscribed in an isosceles right triangle so that the square and the triangle have one... A rectangle is inscribed in a square creation for isosceles right triangle. Square Inscribed in a Right Triangle. Geometry video. Inscribed Circle of an Isosceles Right Triangle Find the side length of an inscribed square in a 'Right Triangle' | Similar triangles || Similarity A Rectangle is Inscribed in an Isosceles Triangle - Maximize the Area! A square inscribed in a triangle 1 A circle is inscribed in the region between a quarter circle and an isosceles right triangle finding the side length of a square inscribed in a right triangle A square is incribed in an isoceles right triangle, so that the square and the triangle have one... Geometry! What is the area above a circle inscribed in an isosceles triangle?? Inscribing a square, a quarter circle and a triangle in a rectangle Three square on an isosceles right triangle Geometry, Level 2 of 6, Example 1, Square inscribed by right triangle Find square value of a side of an isosceles triangle The figure shows a rectangle inscribed in an isosceles right triangle whose hypotenuse is 2 units l… A circle is inscribed in an isosceles right angle, 4 units length for both sides. Find the radius r. A square and an isosceles triangle. Could you find the value of x? A square is inscribed in a circle with radius = 5, what is the area of the square?

Conclusion

Taking everything into consideration, it is obvious that publication provides beneficial awareness concerning Question 1 A Square Is Inscribed In An Isosceles Right Triangle Have. Throughout the content, the reporter exhibits remarkable understanding regarding the topic. Markedly, the discussion of this element stands out as particularly informative. In addition, the write-up is exceptional in disentangling complex concepts in an plain manner. In addition, the scribe presents tangible illustrations that amplify the engagement. A supplementary feature that makes this piece exceptional is the comprehensive analysis of varied aspects related to Question 1 A Square Is Inscribed In An Isosceles Right Triangle Have. The writers meticulous approach makes certain that observers achieve a thorough comprehension of the subject matter. Thanks for reviewing this write-up. Should you have any questions, please go ahead and connect with me with the comment section. I am enthusiastic about your input. In wrapping up, to learn more, you will find a variety of akin essays that could be helpful:May you find them engaging!