Simple Pendulum Newtonian Lagrangian Hamiltonian Approaches

Newtonian V Lagrangian V Hamiltonian For A Simple Pendulum Youtube Explanation of simple pendulum problem based of newtonian mechanics, lagrangian mechanics and hamiltonian mechanics. The hamiltonian turns up there too. oh, and other places. let’s get started though. i am again skipping the derivation of the hamiltonian. this is a blog post, not a textbook. in one dimension (and for one particle) the hamiltonian is defined as: yes, you have to find the lagrangian first. oh, the p is momentum. however, once you get the.

Simple Pendulum Newtonian Lagrangian Hamiltonian Approaches Youtube Let’s start with a simple example: a particle moving in a potential in 3 dimensional space. the lagrangian is simply l = 1 2 mr˙2 v(r)(4.17) we calculate the momentum by taking the derivative with respect to r˙ p = @l @r˙ = mr˙ (4.18) which, in this case, coincides with what we usually call momentum. the hamiltonian is then given by h = p. 1.3 lagrangian formulation of newtonian mechanics 7 1.4 hamiltonian formulation 8 1.4.1 introduction of the hamiltonian 8 1.4.2 phase space 10 1.5 examples 11 1.5.1 harmonic oscillator 11 1.5.2 simple pendulum 11 1.5.3 exact solution of the pendulum equations 14 1.5.4 a bead on a rotating circle 15 1.5.5 spherical pendulum 18 1.5.6 rigid body. Explore the equations of motion for a simple pendulum through three distinct methods: newtonian, lagrangian, and hamiltonian mechanics in this 39 minute physics video. begin with an introduction, then delve into the newtonian approach, followed by a numerical solution using python. An (5) and the following principle.principle of stationary action (hamilton's principle): the dynamics of a nonlinear dynamical system with lagrangian function (5) makes the action (6) stationary relative to all possible paths q(t) connecting two given admi. the basic idea of hamilton's principle is sketched in figure 1, and it can be expressed.
Newton Lagrange Hamilton Explore the equations of motion for a simple pendulum through three distinct methods: newtonian, lagrangian, and hamiltonian mechanics in this 39 minute physics video. begin with an introduction, then delve into the newtonian approach, followed by a numerical solution using python. An (5) and the following principle.principle of stationary action (hamilton's principle): the dynamics of a nonlinear dynamical system with lagrangian function (5) makes the action (6) stationary relative to all possible paths q(t) connecting two given admi. the basic idea of hamilton's principle is sketched in figure 1, and it can be expressed. Comparison of newtonian, lagrangian and hamiltonian approaches. hamilton’s equations, symplecticity, integrability, chaos. canonical transformations, the hamilton jacobi equation, poisson brackets. lecture 2 the \accelerator" hamiltonian. dynamic maps, symplectic integrators. integrable hamiltonian. The superiority of the lagrangian approach compared to the newtonian approach for solving problems in mechanics is apparent when dealing with holonomic constraint forces. constraint forces must be known and included explicitly in the newtonian equations of motion. unfortunately, knowledge of the equations of motion is required to derive these.
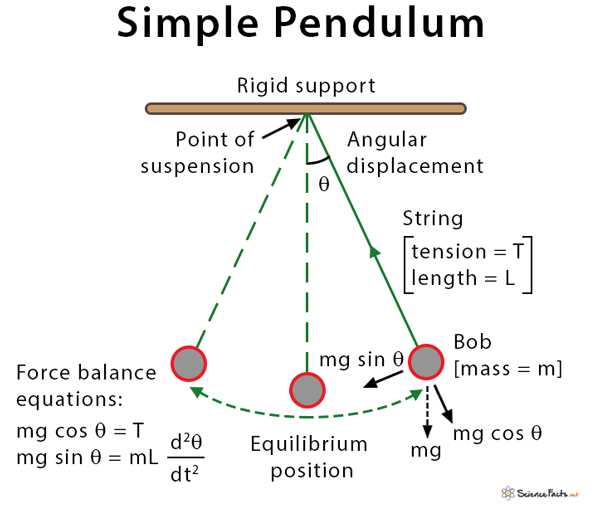
Simple Pendulum Equation Comparison of newtonian, lagrangian and hamiltonian approaches. hamilton’s equations, symplecticity, integrability, chaos. canonical transformations, the hamilton jacobi equation, poisson brackets. lecture 2 the \accelerator" hamiltonian. dynamic maps, symplectic integrators. integrable hamiltonian. The superiority of the lagrangian approach compared to the newtonian approach for solving problems in mechanics is apparent when dealing with holonomic constraint forces. constraint forces must be known and included explicitly in the newtonian equations of motion. unfortunately, knowledge of the equations of motion is required to derive these.

Comments are closed.