Simple Pendulum Theory Diagram And Formula

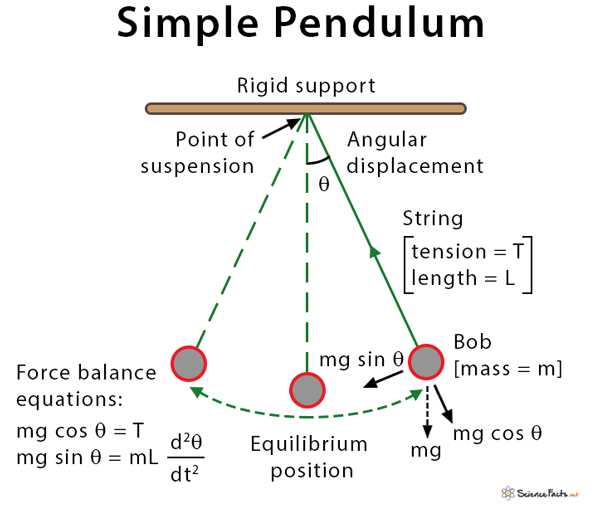
Simple Pendulum Theory Diagram And Formula θ = θ max sin (ωt φ) a simple pendulum is a typical laboratory experiment in many academic curricula. students are often asked to evaluate the value of the acceleration due to gravity, g, using the equation for the time period of a pendulum. rearranging the time period equation, g =4π2 l t 2 g = 4 π 2 l t 2. Figure 16.4.1 16.4. 1: a simple pendulum has a small diameter bob and a string that has a very small mass but is strong enough not to stretch appreciably. the linear displacement from equilibrium is s s, the length of the arc. also shown are the forces on the bob, which result in a net force of mgsinθ m g s i n θ toward the equilibrium.

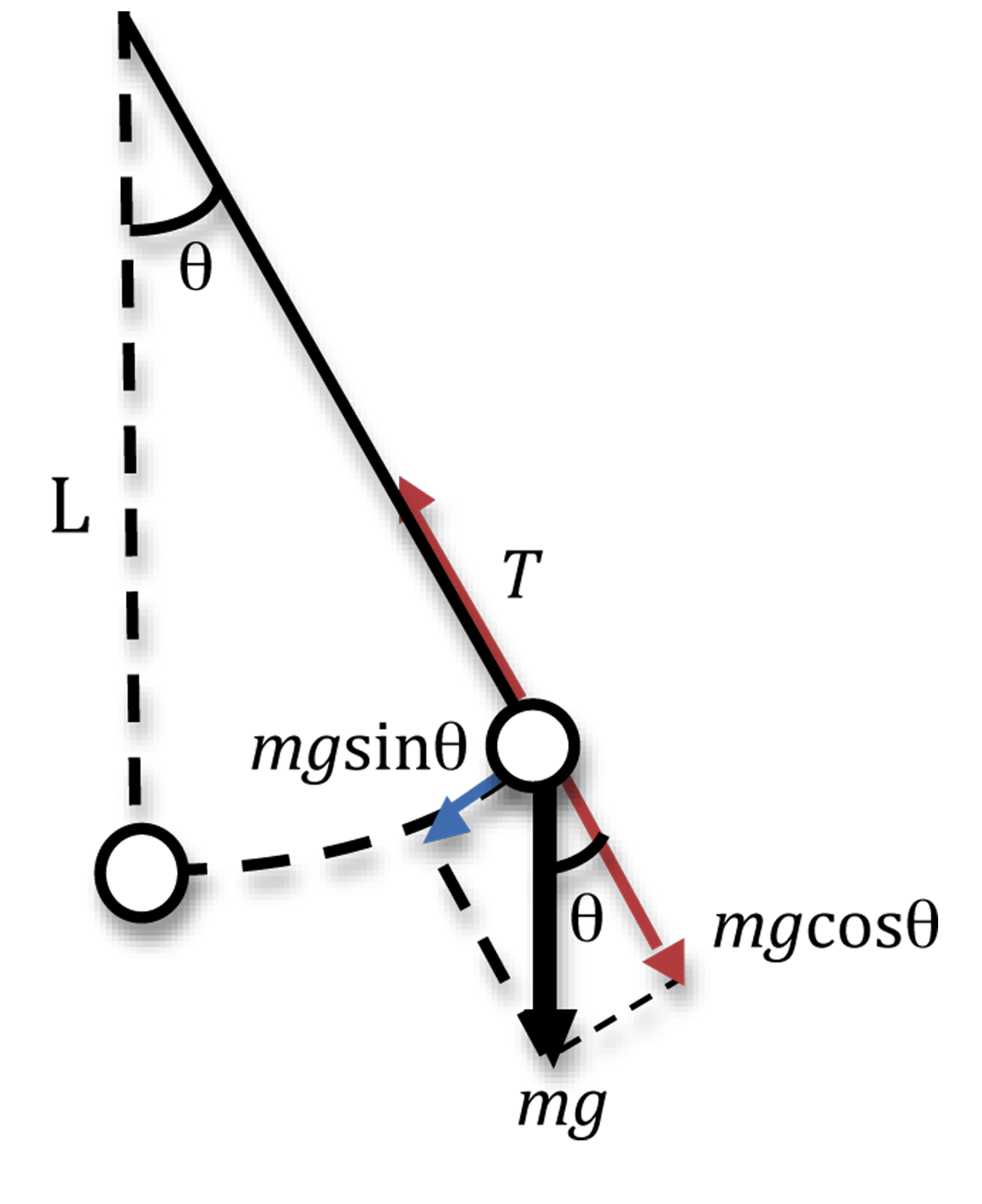
Simple Pendulum Ucsc Physics Demonstration Room The period is completely independent of other factors, such as mass. as with simple harmonic oscillators, the period t t for a pendulum is nearly independent of amplitude, especially if θ θ is less than about 15º 15º. even simple pendulum clocks can be finely adjusted and accurate. note the dependence of t t on g g. if the length of a. Figure 1. a simple pendulum has a small diameter bob and a string that has a very small mass but is strong enough not to stretch appreciably. the linear displacement from equilibrium is s, the length of the arc. also shown are the forces on the bob, which result in a net force of −mg sinθ toward the equilibrium position—that is, a. Using this equation, we can find the period of a pendulum for amplitudes less than about 15º. for the simple pendulum: t =2π√m k = 2π√ m mg l t = 2 π m k = 2 π m m g l. thus, t =2π√l g t = 2 π l g for the period of a simple pendulum. this result is interesting because of its simplicity. A torsional pendulum consists of a rigid body suspended by a light wire or spring (figure 15.5.3 15.5. 3). when the body is twisted some small maximum angle (Θ Θ) and released from rest, the body oscillates between (θ θ = Θ Θ) and (θ θ = − Θ Θ). the restoring torque is supplied by the shearing of the string or wire.

Conservation Of Energy In Simple Pendulum Teachoo Science Using this equation, we can find the period of a pendulum for amplitudes less than about 15º. for the simple pendulum: t =2π√m k = 2π√ m mg l t = 2 π m k = 2 π m m g l. thus, t =2π√l g t = 2 π l g for the period of a simple pendulum. this result is interesting because of its simplicity. A torsional pendulum consists of a rigid body suspended by a light wire or spring (figure 15.5.3 15.5. 3). when the body is twisted some small maximum angle (Θ Θ) and released from rest, the body oscillates between (θ θ = Θ Θ) and (θ θ = − Θ Θ). the restoring torque is supplied by the shearing of the string or wire. The simple pendulum. the lagrangian derivation of the equations of motion (as described in the appendix) of the simple pendulum yields: m l 2 θ ¨ (t) m g l sin θ (t) = q. we'll consider the case where the generalized force, q, models a damping torque (from friction) plus a control torque input, u (t): q = − b θ ˙ (t) u (t). Figure 1. a simple pendulum has a small diameter bob and a string that has a very small mass but is strong enough not to stretch appreciably. the linear displacement from equilibrium is s, the length of the arc. also shown are the forces on the bob, which result in a net force of −mg sinθ toward the equilibrium position—that is, a.

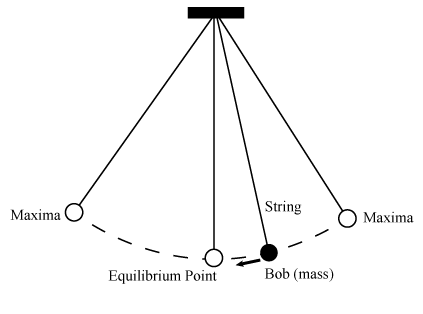
Simple Pendulum The simple pendulum. the lagrangian derivation of the equations of motion (as described in the appendix) of the simple pendulum yields: m l 2 θ ¨ (t) m g l sin θ (t) = q. we'll consider the case where the generalized force, q, models a damping torque (from friction) plus a control torque input, u (t): q = − b θ ˙ (t) u (t). Figure 1. a simple pendulum has a small diameter bob and a string that has a very small mass but is strong enough not to stretch appreciably. the linear displacement from equilibrium is s, the length of the arc. also shown are the forces on the bob, which result in a net force of −mg sinθ toward the equilibrium position—that is, a.