Slope And Deflection Formula For Cantilever Beam The Best Picture O
Slope And Deflection Formula For Cantilever Beam The Best Picture Of Beam To calculate this: choose formula: pl³ (48ei). enter values: 45 × 10³ × (4 × 10³)³ (48 × 2.4 × 10⁵ × 72 × 10⁶) = 3.47 mm. this beam deflection calculator will help you determine the maximum beam deflection of simply supported or cantilever beams subjected to simple load configurations. Example cantilever beam with single load at the end, metric units. the maximum moment at the fixed end of a ub 305 x 127 x 42 beam steel flange cantilever beam 5000 mm long, with moment of inertia 8196 cm 4 (81960000 mm 4), modulus of elasticity 200 gpa (200000 n mm 2) and with a single load 3000 n at the end can be calculated as. m max.
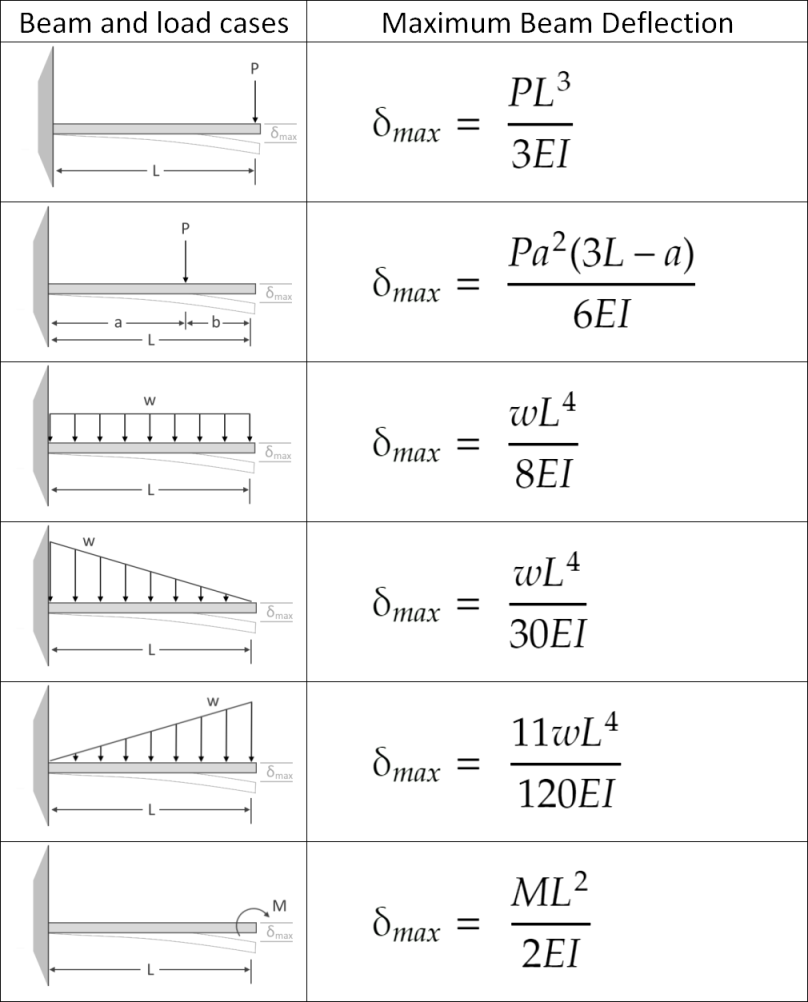
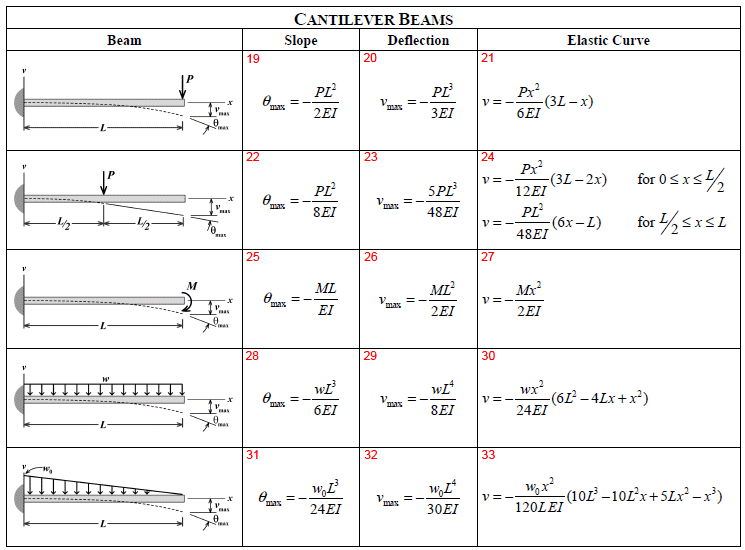
Maximum Deflection Formula For Cantilever Beam The Best Picture Of Beam Where: \ (m x \) = bending moment at point x \ (p \) = load applied at the end of the cantilever \ (x \) = distance from the fixed end (support point) to point of interest along the length of the beam. for a distributed load, the equation would change to: \ (m x = – ∫wx\) over the length (x1 to x2) where: w = distributed load x1 and x2 are. Propped cantilever beam. consider the propped cantilever beam shown in figure 11.5. the slope deflection equations for the end moments are as follows: solving equation 11.13 for θ b and substituting it into equation 11.12 suggests the following: equation 11.14 is the modified slope deflection equation when the far end is supported by a pin or. Beam deflection formulae beam type slope at free end deflection at any section in terms of x maximum deflection 1. cantilever beam – concentrated load p at the free end 2 pl 2 e i (n m) 2 3 px ylx 6 ei 24 3 max pl 3 e i max 2. cantilever beam – concentrated load p at any point 2 pa 2 e i lei 2 3for0 px yax xa 6 ei 2 3for pa yxaaxl 6 ei 2 3. A beam carries a distributed load that varies from zero at support a to 50 kn m at its overhanging end, as shown in figure 7.4a.write the equation of the elastic curve for segment ab of the beam, determine the slope at support a, and determine the deflection at a point of the beam located 3 m from support a.

Beam Slope And Deflection Table Structural Analysis Engineering In Beam deflection formulae beam type slope at free end deflection at any section in terms of x maximum deflection 1. cantilever beam – concentrated load p at the free end 2 pl 2 e i (n m) 2 3 px ylx 6 ei 24 3 max pl 3 e i max 2. cantilever beam – concentrated load p at any point 2 pa 2 e i lei 2 3for0 px yax xa 6 ei 2 3for pa yxaaxl 6 ei 2 3. A beam carries a distributed load that varies from zero at support a to 50 kn m at its overhanging end, as shown in figure 7.4a.write the equation of the elastic curve for segment ab of the beam, determine the slope at support a, and determine the deflection at a point of the beam located 3 m from support a. Beam design formulas. simply select the picture which most resembles the beam configuration and loading condition you are interested in for a detailed summary of all the structural properties. beam equations for resultant forces, shear forces, bending moments and deflection can be found for each beam case shown. This video explains how to find out the slope & deflection in case of cantilever beam carrying uniformly distributed load & point load, using the macaulay's.

Cantilever Beam Deflection Formula S Youtube Beam design formulas. simply select the picture which most resembles the beam configuration and loading condition you are interested in for a detailed summary of all the structural properties. beam equations for resultant forces, shear forces, bending moments and deflection can be found for each beam case shown. This video explains how to find out the slope & deflection in case of cantilever beam carrying uniformly distributed load & point load, using the macaulay's.

Comments are closed.