Soddy Circles And Descartes Theorem Three Tangent Circles Ipad Apps

Soddy Circles And Descartes Theorem Three Tangent Circles Ipad Apps This formula is called the descartes circle theorem since it was known to rene descartes (1596 1650). frederic soddy (1936) extended the result to tangent spheres. typography art in motion using mobile apps, ipad. A special case of descartes' theorem on the sphere has three circles of radius 60° (k = 1 √3, in blue) for which both circles touching all three (in green) have the same radius (30°, k = √3). descartes' theorem generalizes to mutually tangent great or small circles in spherical geometry if the curvature of the th circle is defined as.

Go Geometry Soddy Circles And Descartes Theorem Three Tangent Circles Descartes' circle theorem (a.k.a. the kissing circle theorem) provides a quadratic equation satisfied by the radii of four mutually tangent circles. by solving this equation, one can determine the possible values for the radius of a fourth circle tangent to three given, mutually tangent circles. the theorem was first stated in a 1643 letter from rené descartes to princess elizabeth of. Given three noncollinear points, construct three tangent circles such that one is centered at each point and the circles are pairwise tangent to one another. then there exist exactly two nonintersecting circles that are tangent to all three circles. these are called the inner and outer soddy circles, and their centers are called the inner s and outer soddy centers s^', respectively. frederick. Online geometry theorems, problems, solutions, and related topics. friday, december 30, 2016. soddy circles and descartes theorem, three tangent circles. A special case of apollonius' problem requiring the determination of a circle touching three mutually tangent circles (also called the kissing circles problem). there are two solutions: a small circle surrounded by the three original circles, and a large circle surrounding the original three. frederick soddy gave the formula for finding the radius of the so called inner and outer soddy circles.
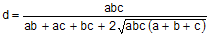
Soddy Circles And Descartes Theorem Three Tangent Circles Ipad Apps Online geometry theorems, problems, solutions, and related topics. friday, december 30, 2016. soddy circles and descartes theorem, three tangent circles. A special case of apollonius' problem requiring the determination of a circle touching three mutually tangent circles (also called the kissing circles problem). there are two solutions: a small circle surrounded by the three original circles, and a large circle surrounding the original three. frederick soddy gave the formula for finding the radius of the so called inner and outer soddy circles. 28. ( 11 21 24 28)2 = 622 = 3844. 2(( 11)2 212 242 282) = 2(1922) = 3844 1643 { rene descartes wrote the theorem and an incomplete proof of it in a letter to princess elisabeth of bohemia. 1826 { jakob steiner independently rediscovered the theorem and provided a complete proof of it. 1842 { philip beecroft independently. Circle tangent to three tangent circles (without the soddy descartes formula) we have three circles tangent to each other with radii $1$, $2$, and $3$. another circle is tangent to the other circles; find the radius of that circle using elementary geometry, without the soddy.

Problem Solving With Gsp Three Tangent Circles Soddy Circles Youtube 28. ( 11 21 24 28)2 = 622 = 3844. 2(( 11)2 212 242 282) = 2(1922) = 3844 1643 { rene descartes wrote the theorem and an incomplete proof of it in a letter to princess elisabeth of bohemia. 1826 { jakob steiner independently rediscovered the theorem and provided a complete proof of it. 1842 { philip beecroft independently. Circle tangent to three tangent circles (without the soddy descartes formula) we have three circles tangent to each other with radii $1$, $2$, and $3$. another circle is tangent to the other circles; find the radius of that circle using elementary geometry, without the soddy.

Comments are closed.