Solved 13 A Square With Side Length 3 Is Inscribed In An Isosceles

Solved 13 A Square With Side Length 3 Is Inscribed In An Isosceles Because cuts the side length of the square in half; similarly, . let : then by side ratios, . now the height of the triangle is . by side ratios, . the area of the triangle is ~kingravi solution 2. by similarity, the height is and the base is . thus the area is . ~hefei417, or 陆畅 sunny from china solution 3 (with two different endings). A square with side length 3 is inscribed in an isosceles triangle with one side of the square along the base of the triangle. a square with side length 2 has two vertices on the other square and the other two on sides of the triangle, as shown. what is the area of the triangle? 3 3 (a) 1953 (b): (b) 20(c) 21; (d) 22 (e) 23% 4.
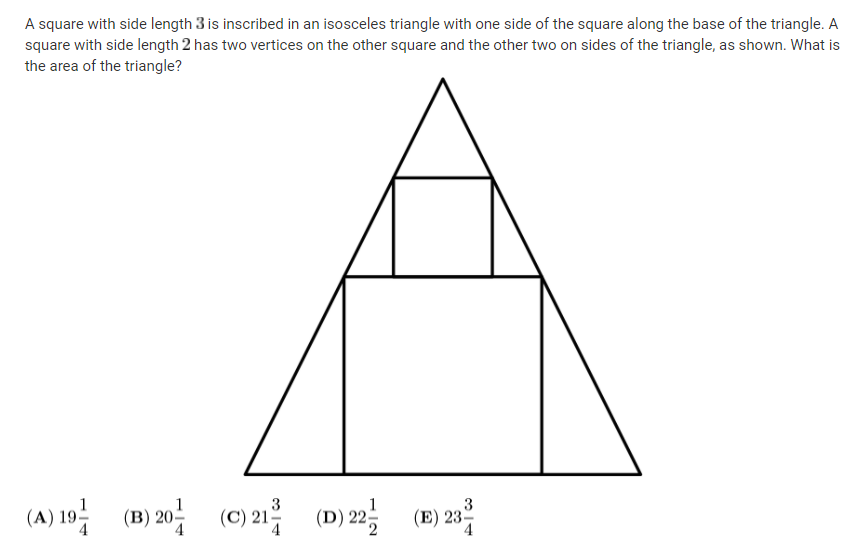
Solved A Square With Side Length 3 Is Inscribed In An Chegg A square with side length has two vertices on the other square and the other two on sides of the triangle as shown. what is the area of the triangle? (a) 194 (b) 1204 (c) 21 (d) 223 (e) 24 13. a square with side length 3 is inscribed in an isosceles triangle with one side of the square along the base of the triangle. 13. a square with side length 3 is inscribed in an isosceles triangle with one side of the square along the base of the triangle. a square with side length 2 has two vertices on the other square and the other two on sides of the triangle, as shown. what is the area of the triangle? (b) 20 (c) 21 () 22 (c)21 (e) 23. calculus: early. To calculate the isosceles triangle area, you can use many different formulas. the most popular ones are the equations: given leg a and base b: area = (1 4) × b × √( 4 × a² b² ) given h height from apex and base b or h2 height from the other two vertices and leg a: area = 0.5 × h × b = 0.5 × h2 × a. given any angle and leg or base. Solution. we are given that the area of the inscribed square is , so the side length of that square is . since the square divides the larger triangle into 2 smaller congruent , then the legs of the larger isosceles right triangle ( and ) are equal to . we now have that , so . but we want the area of the square which is.

Isosceles Triangle Side Lengths To calculate the isosceles triangle area, you can use many different formulas. the most popular ones are the equations: given leg a and base b: area = (1 4) × b × √( 4 × a² b² ) given h height from apex and base b or h2 height from the other two vertices and leg a: area = 0.5 × h × b = 0.5 × h2 × a. given any angle and leg or base. Solution. we are given that the area of the inscribed square is , so the side length of that square is . since the square divides the larger triangle into 2 smaller congruent , then the legs of the larger isosceles right triangle ( and ) are equal to . we now have that , so . but we want the area of the square which is. 1. there is an isosceles triangle with base a = 10 a = 10 and sides b = 13 b = 13. a square is inscribed inside of this triangle such that two of it's vertices are touching base and two of them are touching sides. what is the length of a side of the square? the solution is 60 11 60 11, but i don't know how to arrive at it. geometry. triangles. 13. a square with side length 3 is inscribed in an isosceles triangle with one side of the square along the base of the triangle. a square with side length 2 has two vertices on the other square and the other two on sides of the triangle, as shown. what is the area of the triangle? (a) 19 (b) 20 (c) 21 (d) 22 (e) 23 4 4 4 ni.
Isosceles Triangle Formula Angle At Michelle Stingley Blog 1. there is an isosceles triangle with base a = 10 a = 10 and sides b = 13 b = 13. a square is inscribed inside of this triangle such that two of it's vertices are touching base and two of them are touching sides. what is the length of a side of the square? the solution is 60 11 60 11, but i don't know how to arrive at it. geometry. triangles. 13. a square with side length 3 is inscribed in an isosceles triangle with one side of the square along the base of the triangle. a square with side length 2 has two vertices on the other square and the other two on sides of the triangle, as shown. what is the area of the triangle? (a) 19 (b) 20 (c) 21 (d) 22 (e) 23 4 4 4 ni.

Solved A Square Has Sides 13 Units Squares Of 3 By3 Units Chegg
Isosceles Triangle Side Lengths

Comments are closed.