Solved 2 A Square Is Inscribed In A Right Triangle With Chegg

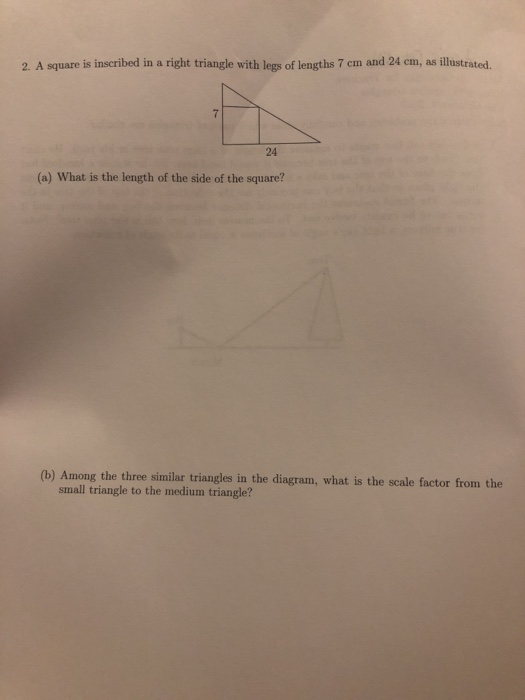
Solved 2 A Square Is Inscribed In A Right Triangle With Chegg Geometry questions and answers. 2. a square is inscribed in a right triangle with legs of lengths 7 cm and 24 cm, as illustrated. (a) what is the length of the side of the square? (b) among the three similar triangles in the diagram, what is the scale factor from the small triangle to the medium triangle?. Question: problem:a square is inscribed in a right triangle, as shown below. find the area of the square.a square is inscribed in a right triangle abc, if ab =1, and bc=3. find the area of the square.

Solved A Square Is Inscribed In A Right Triangle As Shown Chegg Let side of square = s ac = b, bc = a, ab = c. fb = as b and ae = bs a as the colored triangles are similar to the bigger triangle. steps to calculate area (s^2) : 1)calculate gb and ad using right angle triangle rule for triangles gbf and ade. 2)calculate gd using right angle triangle rule for triangle gcd. 3) gd^2 = s^2. The 45° 45° 90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45° 45° 90°, follow a ratio of 1:1:√ 2. like the 30° 60° 90° triangle, knowing one side length allows you to determine the lengths of the other sides. In this video i show how to find the side length of a square inscribed in a right triangle. the concepts covered in this video include similar triangles, rat. I found this two equations to solve the problem. first of all, x2 y2 = 16 x 2 y 2 = 16 (considering pythagore's theorem). then you can easily find a relation such as x. y = x y x. y = x y using either thales' theorem or the fact that the right triangle include two little triangle of heigth 1 and of base x and y respectivly.

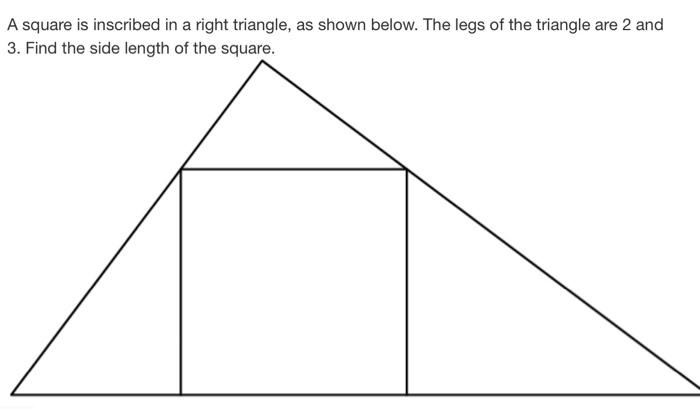
Solved 2 Right Triangle In A Right Triangle The Square Of Chegg In this video i show how to find the side length of a square inscribed in a right triangle. the concepts covered in this video include similar triangles, rat. I found this two equations to solve the problem. first of all, x2 y2 = 16 x 2 y 2 = 16 (considering pythagore's theorem). then you can easily find a relation such as x. y = x y x. y = x y using either thales' theorem or the fact that the right triangle include two little triangle of heigth 1 and of base x and y respectivly. Figure 1 and figure 2 each show a square inscribed in a right triangle. assume the triangles, both labeled abc, are congruent, or two copies of the same triangle. 1. given any right triangle with sides of length a, b, and c, as above, determine the two constructions to inscribe these squares in the right triangle. hint for figure 1. There are 2 steps to solve this one. a square is inscribed in a right triangle. the legs of the triangle are 2 and 3. a square is inscribed in a right triangle, as shown below. the legs of the triangle are 2 and 3. find the side length of the square.