Solved 4 A Calculate The Moment Of Inertia Of The Triangle Shown In
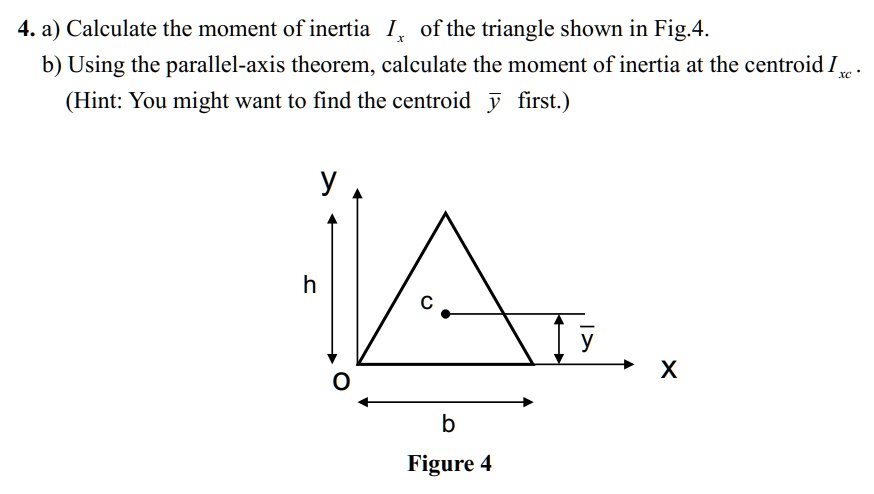
Solved 4 A Calculate The Moment Of Inertia Of The Triangle Shown In This problem has been solved! you'll get a detailed solution from a subject matter expert that helps you learn core concepts. question: 4. a) calculate the moment of inertia of the triangle shown in fig.4. b) using the parallel axis theorem, calculate the moment of inertia at the centroid i, (hint: you might want to find the centroid y rc first.). Step 1. calculate the moment of inertia of the triangular area shown with respect to the x x centroidal axis and with respect of the base of the triangle. round to the nearest whole number. 12" x x 8" in 4 with respect to the centroidal axis: the moment of inertia is with respect to the base of the triangle: the moment of inertia is ing.

Solved Determine The Moment Of Inertia For The Triangle Chegg Next, we calculate the moment of inertia for the same uniform thin rod but with a different axis choice so we can compare the results. we would expect the moment of inertia to be smaller about an axis through the center of mass than the endpoint axis, just as it was for the barbell example at the start of this section. I1 = mr2 mr2 = 2mr2. (10.6.2) in the case with the axis at the end of the barbell—passing through one of the masses—the moment of inertia is. i2 = m(0)2 m(2r)2 = 4mr2. (10.6.3) from this result, we can conclude that it is twice as hard to rotate the barbell about the end than about its center. The moment of inertia of a triangle with respect to an axis perpendicular to its base, can be found, considering that axis y' y' in the figure below, divides the original triangle into two right ones, a and b. these triangles, have common base equal to h, and heights b1 and b2 respectively. thus their combined moment of inertia is: taking into. The differential area of a circular ring is the circumference of a circle of radius ρ times the thickness dρ. da = 2πρ dρ. adapting the basic formula for the polar moment of inertia (10.1.5) to our labels, and noting that limits of integration are from ρ = 0 to ρ = r, we get. jo = ∫ar2 da → jo = ∫r 0ρ2 2πρ dρ.

Solved Determine The Moment Of Inertia For The Triangle Chegg The moment of inertia of a triangle with respect to an axis perpendicular to its base, can be found, considering that axis y' y' in the figure below, divides the original triangle into two right ones, a and b. these triangles, have common base equal to h, and heights b1 and b2 respectively. thus their combined moment of inertia is: taking into. The differential area of a circular ring is the circumference of a circle of radius ρ times the thickness dρ. da = 2πρ dρ. adapting the basic formula for the polar moment of inertia (10.1.5) to our labels, and noting that limits of integration are from ρ = 0 to ρ = r, we get. jo = ∫ar2 da → jo = ∫r 0ρ2 2πρ dρ. The moment of inertia of a triangle having its axis passing through the centroid and parallel to its base is expressed as; i = bh 3 36. here, b = base width and h = height. 2. axis passing through the base. if we take the axis that passes through the base, the moment of inertia of a triangle is given as; i = bh 3 12. Using the formula for moment of inertia, we can calculate the moment of inertia of the rectangle as follows: i = (b * h^3) 12 i = (2 * 4^3) 12i = (2 * 64) 12 = 10.67 in^4. so the moment of inertia of the rectangle is 10.67 inch^4.
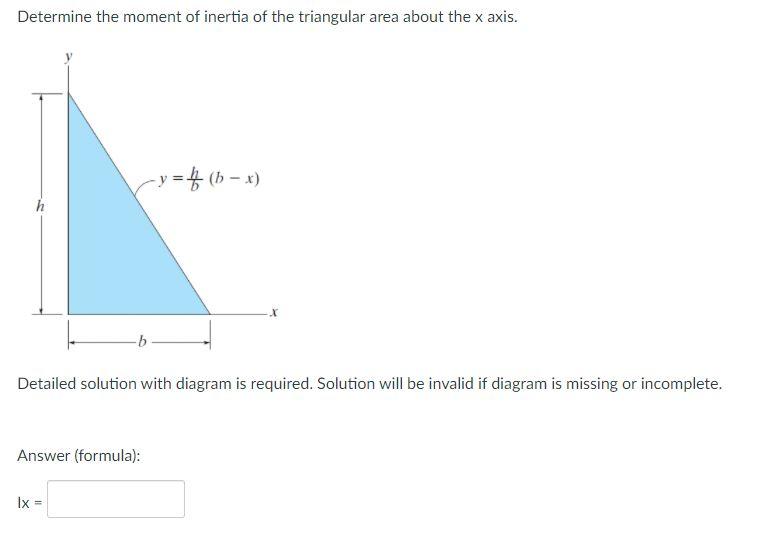
Solved Determine The Moment Of Inertia Of The Triangular Chegg The moment of inertia of a triangle having its axis passing through the centroid and parallel to its base is expressed as; i = bh 3 36. here, b = base width and h = height. 2. axis passing through the base. if we take the axis that passes through the base, the moment of inertia of a triangle is given as; i = bh 3 12. Using the formula for moment of inertia, we can calculate the moment of inertia of the rectangle as follows: i = (b * h^3) 12 i = (2 * 4^3) 12i = (2 * 64) 12 = 10.67 in^4. so the moment of inertia of the rectangle is 10.67 inch^4.
Solved Part A Moment Of Inertia Of A Triangle With Respect Chegg

Comments are closed.