Solved A Square With Side Length 3 Is Inscribed In An Chegg
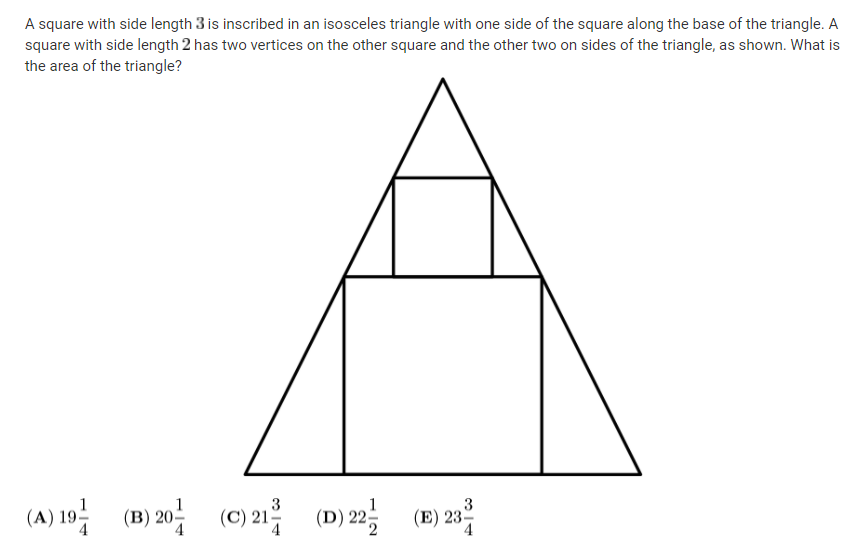
Solved A Square With Side Length 3 Is Inscribed In An Chegg A square with side length 3 is inscribed in an isosceles triangle with one side of the square along the base of the triangle. a square with side length 2 has two vertices on the other square and the other two on sides of the triangle, as shown. what is the area of the triangle? 3 3 (a) 1953 (b): (b) 20(c) 21; (d) 22 (e) 23% 4. Answer to solved a circle has a square of side length s=3 inscribed | chegg . skip to main content there’s just one step to solve this. step 1.

Solved 3 In The Figure Above A Square With A Side Of Length Chegg Here’s the best way to solve it. first square: triangle ade is similar to triangle abc so sides of triangle ade will be 3a, 4a and 5a. 4a = x a = x 4 so 5a …. 1. a square with side length x is inscribed in a right triangle with sides of length 3, 4, and 5 so that one vertex of the square coincides with the right angle vertex of the triangle. The square's area is side length squared, so it is 4r 2. the perimeter is 4 times the side length, so it is 8r. and the length of the diagonal can be calculated using the pythagorean theorem, and it is 2r√2. now let’s do the converse, finding the inscribed circle’s properties from the length of the side of the square. problem 2. If we have a circle of radius 10 cm, then we can do the following to find the largest square inscribed in the circle: the largest square inscribed in a circle of radius r will have a side length of r√2. so for a circle of radius 10 cm, the largest square in it will have a side length of 10√2 cm. this value of the side length can be. A quarter circle of radius 10cm is drawn with the vertex of the square as its centre.find the shaded area.r=10cm. the diagram shows a circle inscribed inside a square of side length 1 0 c m. a quarter circle of radius 1 0 c m is drawn with the vertex of the square as its centre. find the shaded area. there are 3 steps to solve this one.
Solved The Length Of Each Side Of A Square Is 3 In More Chegg If we have a circle of radius 10 cm, then we can do the following to find the largest square inscribed in the circle: the largest square inscribed in a circle of radius r will have a side length of r√2. so for a circle of radius 10 cm, the largest square in it will have a side length of 10√2 cm. this value of the side length can be. A quarter circle of radius 10cm is drawn with the vertex of the square as its centre.find the shaded area.r=10cm. the diagram shows a circle inscribed inside a square of side length 1 0 c m. a quarter circle of radius 1 0 c m is drawn with the vertex of the square as its centre. find the shaded area. there are 3 steps to solve this one. A square is a convex quadrilateral with all sides equal length and positioned at right angles to each other. or, a square is a regular polygon with four sides, a tetragon. area of a square: a = a 2. perimeter of a square. p = 4a. polygon diagonals of a square. q = √(2a 2) = a√2. side of a square . a = √a. A circle is inscribed in a square with a side length of 98 . if a point in the square is chosen at random, what is the probability that the point is inside the circle? there are 3 steps to solve this one.

Solved 3 Square Game Imagine You Have A Square With Side Chegg A square is a convex quadrilateral with all sides equal length and positioned at right angles to each other. or, a square is a regular polygon with four sides, a tetragon. area of a square: a = a 2. perimeter of a square. p = 4a. polygon diagonals of a square. q = √(2a 2) = a√2. side of a square . a = √a. A circle is inscribed in a square with a side length of 98 . if a point in the square is chosen at random, what is the probability that the point is inside the circle? there are 3 steps to solve this one.

Comments are closed.