Solved The Hamiltonian Of A Simple Pendulum Consisting Of A Chegg

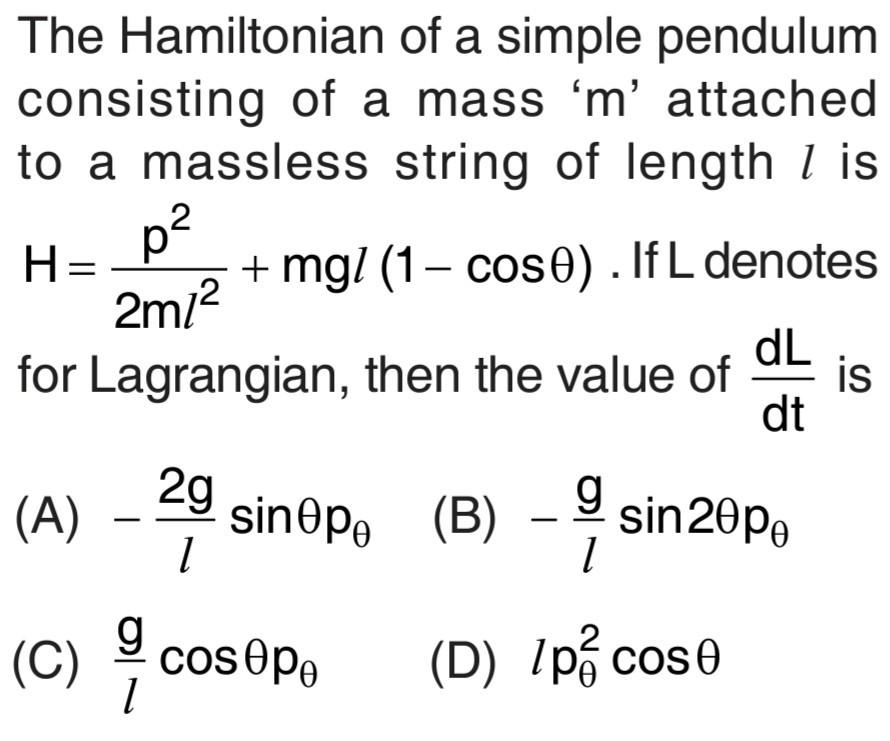
Solved The Hamiltonian Of A Simple Pendulum Consisting Of A Chegg Science. physics. physics questions and answers. the hamiltonian of a simple pendulum consisting of a mass ' m ' attached to a massless string of length l is h=2 ml2p2 mgl (1−cosθ). if l denotes for lagrangian, then the value of dtdl is (a) −l2gsinθpθ (b) −lgsin2θpθ (c) lgcosθpθ (d) lpθ2cosθ. Question: a simple pendulum consisting of a bob of mass m=0.25 kg attached to a string of length l=1.16m. a simple pendulum consisting of a bob of mass m = 0. 2 5 kg attached to a string of length l = 1. 1 6 m. here’s the best way to solve it.

Solved 2ml 14 The Hamiltonian H For A Simple Pendulum Of Chegg Figure 24.2 physical pendulum the gravitational force acts at the center of mass of the physical pendulum. denote the distance of the center of mass to the pivot point s by l . the torque analysis is nearly. cm. identical to the simple pendulum. the torque about the pivot point s is given by. τ = . H = p2 2mr2 mgr(1 − cos θ) h = p 2 2 m r 2 m g r (1 − cos. ⁡. θ) now hamilton's equations will be: p˙ = −mgr sin θ p ˙ = − m g r sin θ. θ˙ = p mr2 θ ˙ = p m r 2. i know one of the points of hamiltonian formalism is to get first order diff. equations instead of second order that lagrangian formalism gives you, but how can. Figure 16.4.1 16.4. 1: a simple pendulum has a small diameter bob and a string that has a very small mass but is strong enough not to stretch appreciably. the linear displacement from equilibrium is s s, the length of the arc. also shown are the forces on the bob, which result in a net force of mgsinθ m g s i n θ toward the equilibrium. I am unable to understand how to put the equation of the simple pendulum in the generalized coordinates and generalized momenta in order to check if it is or not a hamiltonian system. having. et =ek eu = 1 2ml2θ˙2 mgl(1 − cosθ) e t = e k e u = 1 2 m l 2 θ ˙ 2 m g l (1 − c o s θ) how can i found what are the p p and q q for h(q.

Solved 2 Hamiltonian Of A Pendulum A Pendulum Swings In The Chegg Figure 16.4.1 16.4. 1: a simple pendulum has a small diameter bob and a string that has a very small mass but is strong enough not to stretch appreciably. the linear displacement from equilibrium is s s, the length of the arc. also shown are the forces on the bob, which result in a net force of mgsinθ m g s i n θ toward the equilibrium. I am unable to understand how to put the equation of the simple pendulum in the generalized coordinates and generalized momenta in order to check if it is or not a hamiltonian system. having. et =ek eu = 1 2ml2θ˙2 mgl(1 − cosθ) e t = e k e u = 1 2 m l 2 θ ˙ 2 m g l (1 − c o s θ) how can i found what are the p p and q q for h(q. Question: problem 2) consider a simple pendulum consisting of a bob of mass m suspended by a massless rigid rod of length l. (a) find the hamiltonian of the system by following the prescription given in the textbook. (b) find the hamilton's equations of motion. To obtain the kinetic and potential energy you start with the position vector to the mass point which is: $$\vec{r}=l\,\begin{bmatrix} \sin(\varphi) \\ \cos(\varphi) \\ \end{bmatrix}$$.