Sp Math Squares In Right Angled Isosceles Triangle

Sp Math Squares In Right Angled Isosceles Triangle Find the area. solution: for an isosceles right triangle, the area formula is given by x 2 2 where x is the length of the congruent sides. here, x = 8 units. thus, area = 8 2 2 = 32 square units. therefore, the required area is 32 square units. example 2: the perimeter of an isosceles right triangle is 10 5√2. To find the area of an isosceles right triangle, we use the formula: area = ½ × base × height. in this instance, one of the equal sides is considered the base and the other the height. so, if the two equal sides have a measurement of 4cm, insert the measurements for the base and the height to find the actual area. next, follow these steps:.

What Is An Isosceles Right Angle Triangle Definition Examples Byjus In an isosceles right triangle, the length of the height drawn to the hypotenuse is equal to the length of the inscribed circle’s radius multiplied by the silver ratio (the silver ratio equals the unity plus the square root of two): the inscribed circle of an isosceles right triangle. the right isosceles triangle and its properties. Also, two congruent angles in isosceles right triangle measure 45 degrees each, and the isosceles right triangle is: area of an isosceles right triangle. as we know that the area of a triangle (a) is ½ bh square units. where. b is the base of the triangle. h is the altitude of the triangle. in an isosceles right triangle, two legs are of equal. A right angled triangle (also called a right triangle) has a right angle (90°) in it. the little square in the corner tells us it is a right angled triangle. (i also put 90°, but you don't need to!) the right angled triangle is one of the most useful shapes in all of mathematics! it is used in the pythagoras theorem and sine, cosine and. To calculate the isosceles triangle area, you can use many different formulas. the most popular ones are the equations: given leg a and base b: area = (1 4) × b × √( 4 × a² b² ) given h height from apex and base b or h2 height from the other two vertices and leg a: area = 0.5 × h × b = 0.5 × h2 × a. given any angle and leg or base.
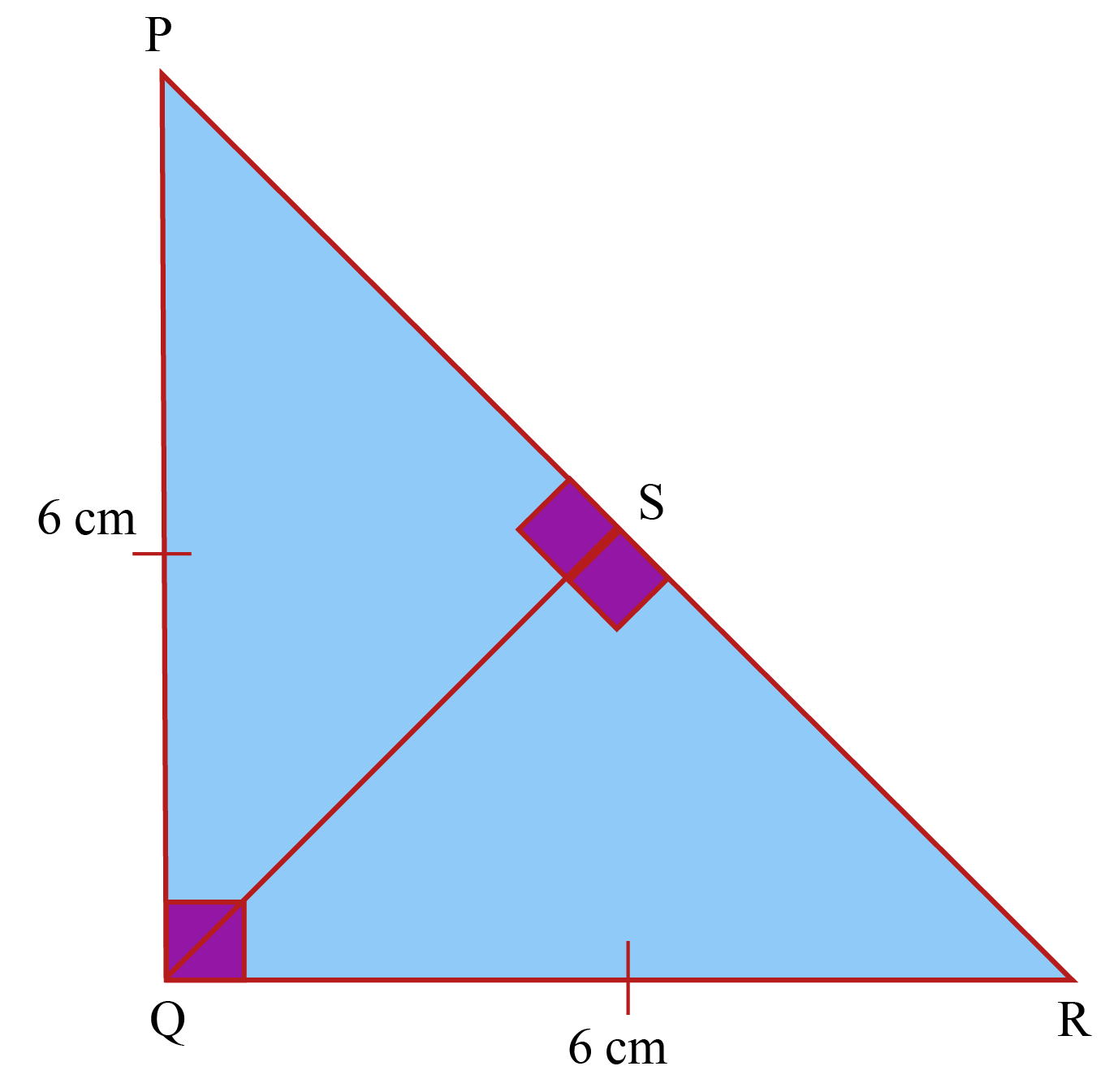
Isosceles Triangle Solved Examples Geometry Cuemath A right angled triangle (also called a right triangle) has a right angle (90°) in it. the little square in the corner tells us it is a right angled triangle. (i also put 90°, but you don't need to!) the right angled triangle is one of the most useful shapes in all of mathematics! it is used in the pythagoras theorem and sine, cosine and. To calculate the isosceles triangle area, you can use many different formulas. the most popular ones are the equations: given leg a and base b: area = (1 4) × b × √( 4 × a² b² ) given h height from apex and base b or h2 height from the other two vertices and leg a: area = 0.5 × h × b = 0.5 × h2 × a. given any angle and leg or base. An isosceles obtuse triangle is a triangle with 2 congruent sides and angles in which the non congruent angle is obtuse. right isosceles triangle. an isosceles right triangle is a triangle with 2 congruent sides and angles in which the non congruent angle measures 90°. because the sum of a triangle's interior angles is equal to 180°, the. This can be represented using the following equation: a=√ (c^2−b^2), with b and c being the lengths of the other two sides. there are also a few different ways to derive an isosceles right triangle. the most common method is to start with a square and draw its diagonal. this creates two smaller squares, each with its own side length and area.
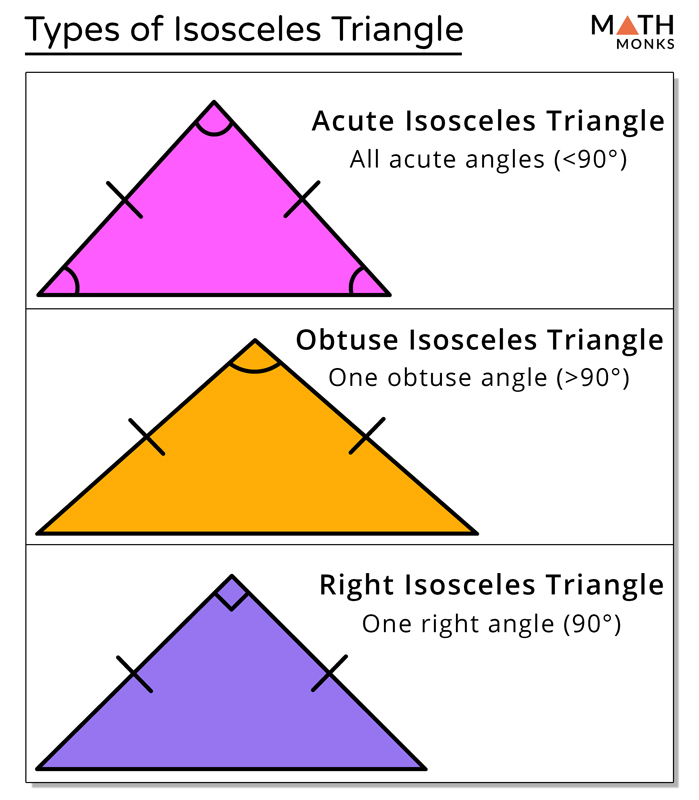
Isosceles Triangle Definition Properties Types Formulas An isosceles obtuse triangle is a triangle with 2 congruent sides and angles in which the non congruent angle is obtuse. right isosceles triangle. an isosceles right triangle is a triangle with 2 congruent sides and angles in which the non congruent angle measures 90°. because the sum of a triangle's interior angles is equal to 180°, the. This can be represented using the following equation: a=√ (c^2−b^2), with b and c being the lengths of the other two sides. there are also a few different ways to derive an isosceles right triangle. the most common method is to start with a square and draw its diagonal. this creates two smaller squares, each with its own side length and area.

Isosceles Triangle Solved Examples Geometry Cuemath

Isosceles Right Triangle Definition Area Perimeter Examples

Comments are closed.