Square Inscribed In Triangle вђ Geogebra
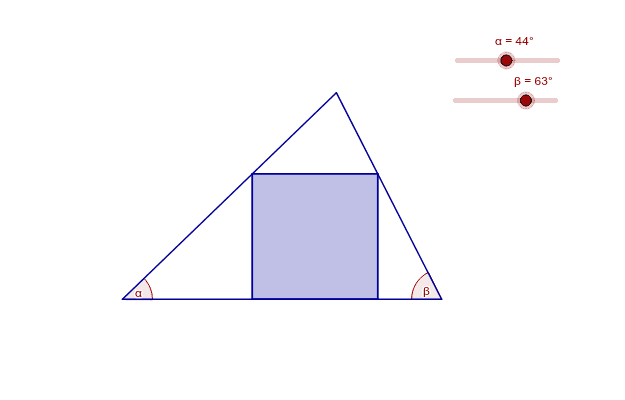
Square Inscribed In Triangle Geogebra Square inscribed in triangle. this was frustrating. much thanks to charlie for his procedural step by step construction directions, but alas i still couldn't get this one. To use this model, we would need to drag point c to make the square larger or smaller. since the square needed to have all of the vertices on the edges of the triangle, i found the point h by creating a line through e parallel to ac. if we drag point d such that ei=eh, i noticed that this would create our desired square. i am still trying to.
Square Inscribed In A Triangle Geogebra A polya example. This is the screencast which shows the procedure to inscribe a square within triangle. Let side of square = s ac = b, bc = a, ab = c. fb = as b and ae = bs a as the colored triangles are similar to the bigger triangle. steps to calculate area (s^2) : 1)calculate gb and ad using right angle triangle rule for triangles gbf and ade. 2)calculate gd using right angle triangle rule for triangle gcd. 3) gd^2 = s^2. The three squares in an equilateral triangle. figure 3. inscribed square in an isosceles triangle. figure 4. isosceles triangle with inscribed square with only one vertex on the side of unique length.
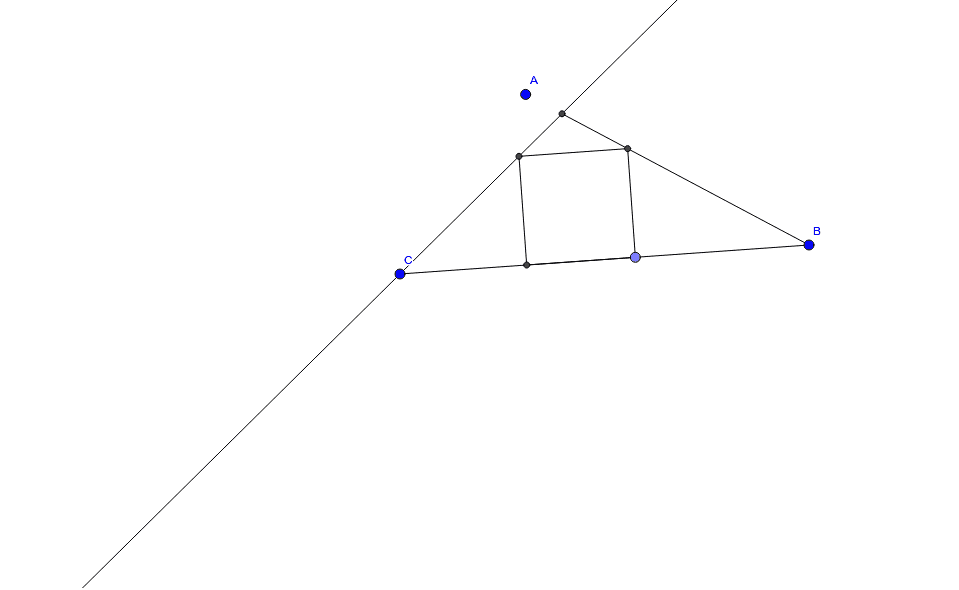
Square Inscribed In Triangle Geogebra Let side of square = s ac = b, bc = a, ab = c. fb = as b and ae = bs a as the colored triangles are similar to the bigger triangle. steps to calculate area (s^2) : 1)calculate gb and ad using right angle triangle rule for triangles gbf and ade. 2)calculate gd using right angle triangle rule for triangle gcd. 3) gd^2 = s^2. The three squares in an equilateral triangle. figure 3. inscribed square in an isosceles triangle. figure 4. isosceles triangle with inscribed square with only one vertex on the side of unique length. Given a triangle deltaabc, an inscribed square is a square all four of whose vertices lie on the edges of deltaabc and two of whose vertices fall on the same edge. as noted by van lamoen (2004), there are two types of squares inscribing reference triangle deltaabc in the sense that all vertices lie on the sidelines of abc. in particular, the first type has two adjacent vertices of the square. Square inscribed in a triangle. discover resources. graph; perpendicular bisectors; tugas pik siska annisa 1600006055 uad3.

Comments are closed.