Tangent To A Circle Definition Equation Theorems Example
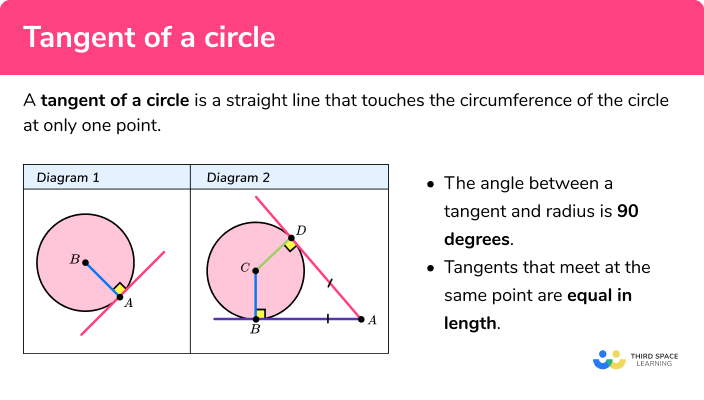
Tangent Of A Circle Gcse Maths Steps Examples Worksheet Note: the tangent to a circle is a special case of the secant when the two endpoints of its corresponding chord coincide. also, read: circles; tangent; equation of tangent and normal; general equation. here, the list of the tangent to the circle equation is given below: the tangent to a circle equation x 2 y 2 =a 2 at (x 1, y 1) is xx 1 yy 1. A c = 15 inches and b c = 25 inches. as we know, the radius and tangent of a circle are perpendicular to each other. in abc, applying pythagoras’ theorem. a c 2 a b 2 = b c 2. 15 2 a b 2 = 25 2. a b 2 = 25 2 − 15 2. a b 2 = 25 2 − 15 2. a b 2 = 400. ∴ a b = 20 inches.
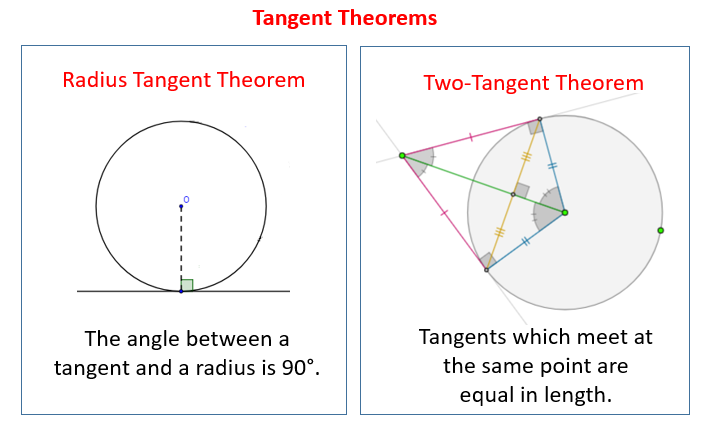
Tangent To Circles Examples Solutions Videos Worksheets Games A tangent to a circle is a line which intersects the circle in exactly one point. in figure 1 line ab←→ a b ↔ is a tangent, intersecting circle o o just at point p p. figure 1. ab←→ a b ↔ is tangent to circle o o at point p p. a tangent has the following important property: theorem 7.3.1 7.3. 1. a tangent is perpendicular to the. Now, we determine the equation of a tangent line to a circle: step 1: firstly find the equation of the circle and write it in the form, (x − a)2 (y − b)2 =r2 (x − a) 2 (y − b) 2 = r 2. step 2: from the above equation, find the coordinates of the centre of the circle (a,b) step 3: find the slope of the radius –. In the given figure, there is one tangent and one secant. given that, pq = 5 cm, qr = 15 cm. therefore, pr = pq qr = (5 15) = 20 cm. now, according to the formula of the tangent of a circle, sr 2 = pr × qr. sr 2 = 20× 15 = 300 = 17.32 cm. find the length of the tangent pr if the radius of the given circle is 6 m. Tangent is a line and to write the equation of a line we need two things, slope (m) and a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1.

Tangent Circle Formula Learn The Formula Of Tangent Circle Along With In the given figure, there is one tangent and one secant. given that, pq = 5 cm, qr = 15 cm. therefore, pr = pq qr = (5 15) = 20 cm. now, according to the formula of the tangent of a circle, sr 2 = pr × qr. sr 2 = 20× 15 = 300 = 17.32 cm. find the length of the tangent pr if the radius of the given circle is 6 m. Tangent is a line and to write the equation of a line we need two things, slope (m) and a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1. Example 2: angles in the same segment. a, b, c, a, b,c, and d d are points on the circumference of a circle with center o. \, ac o.ac and bd b d intersect at point g. \, ef g.ef is a tangent at point c c and is parallel to bd. b d. calculate the size of angle bcf. bcf. locate the key parts of the circle for the theorem. Knowing these essential theorems regarding circles and tangent lines, you are going to be able to identify key components of a circle, determine how many points of intersection, external tangents, and internal tangents two circles have, as well as find the value of segments given the radius and the tangent segment. video – lesson & examples.

Comments are closed.