Tangent To A Circle Formulas Properties Theorems

Tangent Circle Formula Learn The Formula Of Tangent Circle Along With Tangent theorems. there are some theorems based on the tangent of a circle, let’s discuss their statements and proof in detail. theorem 1: tangent radius theorem. the tangent makes a right angle with the radius of a circle at the point of tangency. (at the point of tangency, the tangent is perpendicular to the radius.). Now let a secant is drawn from p to intersect the circle at q and r. ps is the tangent line from point p to s. now, the formula for tangent and secant of the circle could be given as: pr ps = ps pq. ps 2 =pq.pr. tangent theorems. theorem 1: the tangent to the circle is perpendicular to the radius of the circle at the point of contact.
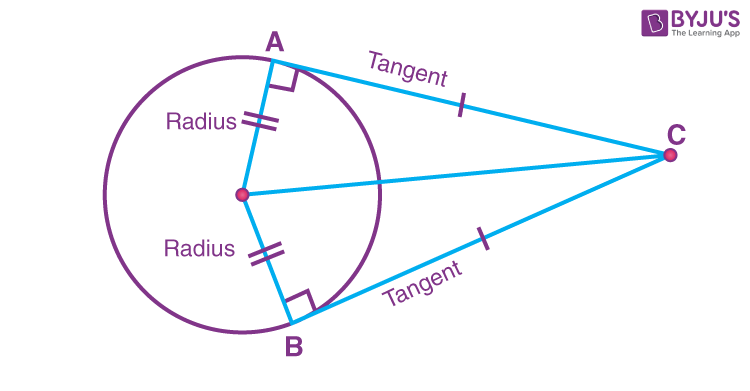
Tangent To A Circle Definition Equation Theorems Example From the same external point, the tangent segments to a circle are equal. learn more about arc of a circle here in detail. download arc of a circle cheat sheet pdf. theorems for tangents to circle theorem 1. a radius is obtained by joining the centre and the point of tangency. the tangent at a point on a circle is at right angles to this radius. A tangent to a circle is a line which intersects the circle in exactly one point. in figure 1 line ab←→ a b ↔ is a tangent, intersecting circle o o just at point p p. figure 1. ab←→ a b ↔ is tangent to circle o o at point p p. a tangent has the following important property: theorem 7.3.1 7.3. 1. a tangent is perpendicular to the. Tangent is a line and to write the equation of a line we need two things, slope (m) and a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1. In the given figure, there is one tangent and one secant. given that, pq = 5 cm, qr = 15 cm. therefore, pr = pq qr = (5 15) = 20 cm. now, according to the formula of the tangent of a circle, sr 2 = pr × qr. sr 2 = 20× 15 = 300 = 17.32 cm. find the length of the tangent pr if the radius of the given circle is 6 m.
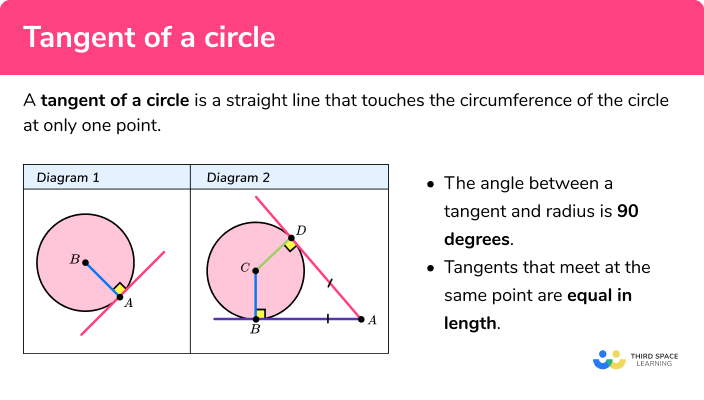
Tangent Of A Circle Gcse Maths Steps Examples Worksheet Tangent is a line and to write the equation of a line we need two things, slope (m) and a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1. In the given figure, there is one tangent and one secant. given that, pq = 5 cm, qr = 15 cm. therefore, pr = pq qr = (5 15) = 20 cm. now, according to the formula of the tangent of a circle, sr 2 = pr × qr. sr 2 = 20× 15 = 300 = 17.32 cm. find the length of the tangent pr if the radius of the given circle is 6 m. Tangent is a line and to write the equation of a line we need two things: 1. slope (m) 2. a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1. In euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. since the tangent line to a circle at a point p is.
Tangent To A Circle Igcse At Mathematics Realm Tangent is a line and to write the equation of a line we need two things: 1. slope (m) 2. a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1. In euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. since the tangent line to a circle at a point p is.

Comments are closed.