Tangents Drawn To A Circle From An External Point
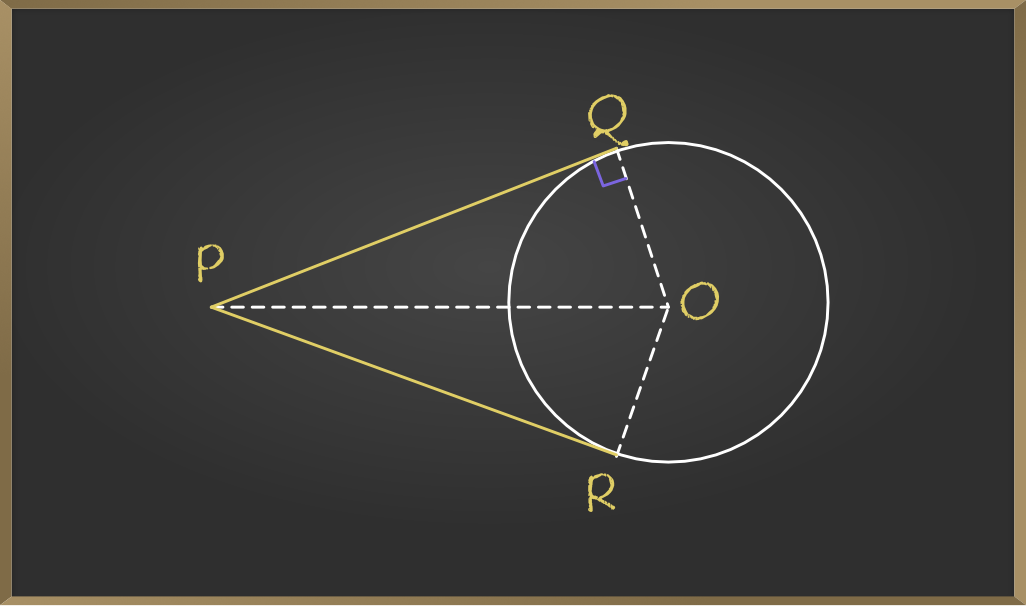
Theorem The Lengths Of Tangents Drawn From An External Point To A A tangent from p has been drawn to s. this is an example of a tangent from an external point: how many tangents do you think can be drawn from an external point to a circle? the answer is two, and the following theorem proves this fact. theorem: exactly two tangents can be drawn from an exterior point to a given circle. consider the following. The tangent makes a right angle at the point of tangency with the radius of a circle. tangents drawn from an external point to a circle have the same length. a circle can have infinitely many tangents. we can draw exactly one tangent to a circle passing through a point that lies on a circle.
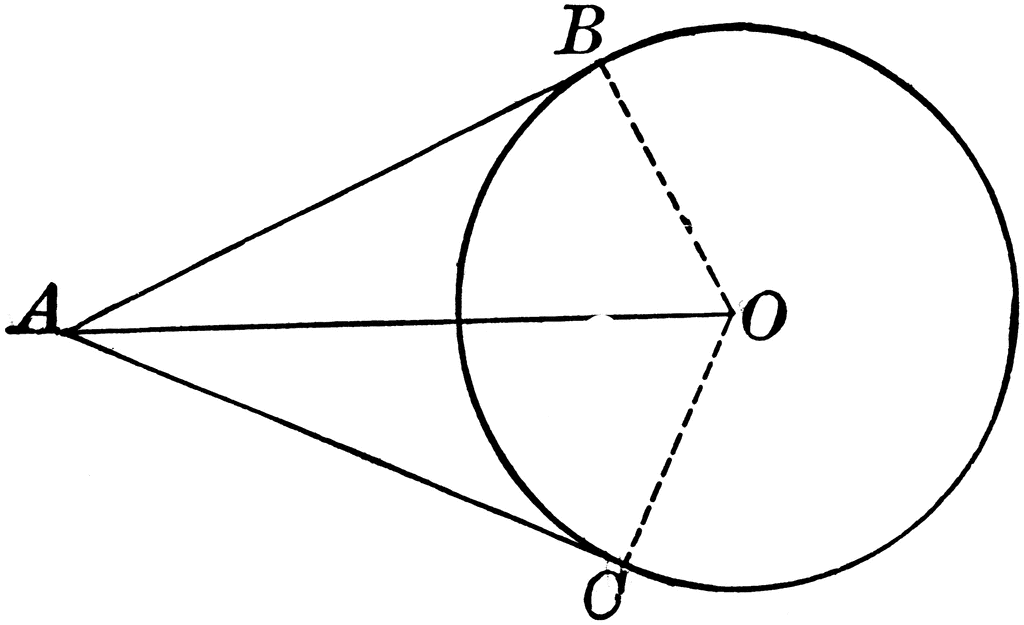
Circle With Two Tangents Drawn From An External Point Clipart Etc From p, fold the paper in such a way that it just touches the circle at p. press it and unfold to get a tangent pa. from a, fold the paper to get tangent aq. fold the circle along oa. join op, oa, oq. thus it is verified that lengths of tangents drawn from an external point to a circle are equal. Transcript. theorem 10.2 (method 1) the lengths of tangents drawn from an external point to a circle are equal. given: let circle be with centre o and p be a point outside circle pq and pr are two tangents to circle intersecting at point q and r respectively to prove: lengths of tangents are equal i.e. pq = pr construction: join oq , or and op proof: as pq is a tangent oq ⊥ pq so, ∠ oqp. Remove parentheses and subtract 360 from both sides: –2∠mjp –2∠ojm = –180. divide through by –2:: ∠mjp ∠ojm = 90. 8. jp is a tangent to circle o and passes through p. jp is a tangent to o because it touches the circle at j and is at right angles to a radius at the contact point. (see tangent to a circle.). The length of tangents from an external point to a circle are equal. tangent formula. suppose a point p lies outside the circle. from that point p, we can draw two tangents to the circle meeting at point a and b. now let a secant is drawn from p to intersect the circle at q and r. ps is the tangent line from point p to s. now, the formula for.
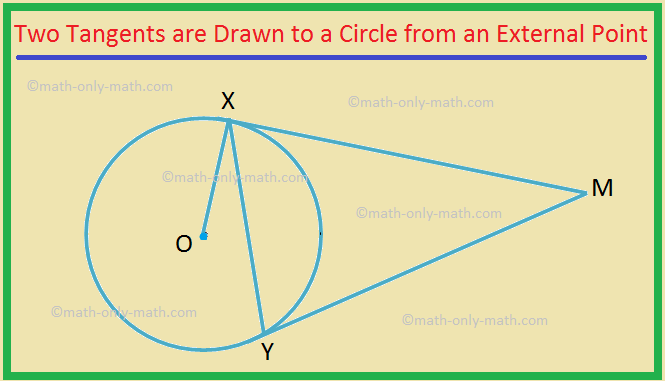
Two Tangents Are Drawn To A Circle From An External Point Proof Remove parentheses and subtract 360 from both sides: –2∠mjp –2∠ojm = –180. divide through by –2:: ∠mjp ∠ojm = 90. 8. jp is a tangent to circle o and passes through p. jp is a tangent to o because it touches the circle at j and is at right angles to a radius at the contact point. (see tangent to a circle.). The length of tangents from an external point to a circle are equal. tangent formula. suppose a point p lies outside the circle. from that point p, we can draw two tangents to the circle meeting at point a and b. now let a secant is drawn from p to intersect the circle at q and r. ps is the tangent line from point p to s. now, the formula for. 3. find the tangent line from an external point (1, 5) to a circle with a radius of 3. answer: the tangent line from (1, 5) to the circle with a radius of 3 is y = 1x 4. 4. find the tangent angle from an external point (2, 4) to a circle with a radius of 6. answer: the tangent angle from (2, 4) to the circle with a radius of 6 is 30 degrees. 5. Ef is a tangent to the circle and the point of tangency is h. tangents from the same external point. two tangent theorem: when two segments are drawn tangent to a circle from the same point outside the circle, the segments are equal in length. in the following diagram: if ab and ac are two tangents to a circle centered at o, then:.

Comments are closed.