Tangents Of Circles
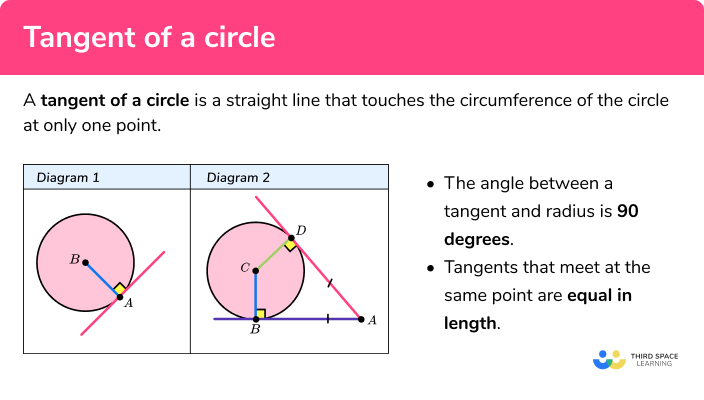
Tangent Of A Circle Gcse Maths Steps Examples Worksheet The tangent of a circle refers to a line that touches a circle at a single point. in the image shown below, the line l is a tangent to the circle with the center c. a straight line that touches or intersects the circle at only one point is called a tangent of the circle. a tangent touches the circle externally. tangent of a circle: definition. Learn what is a tangent to a circle, how to find its equation and properties, and how to apply theorems and formulas. see an example problem and video lessons on circles.
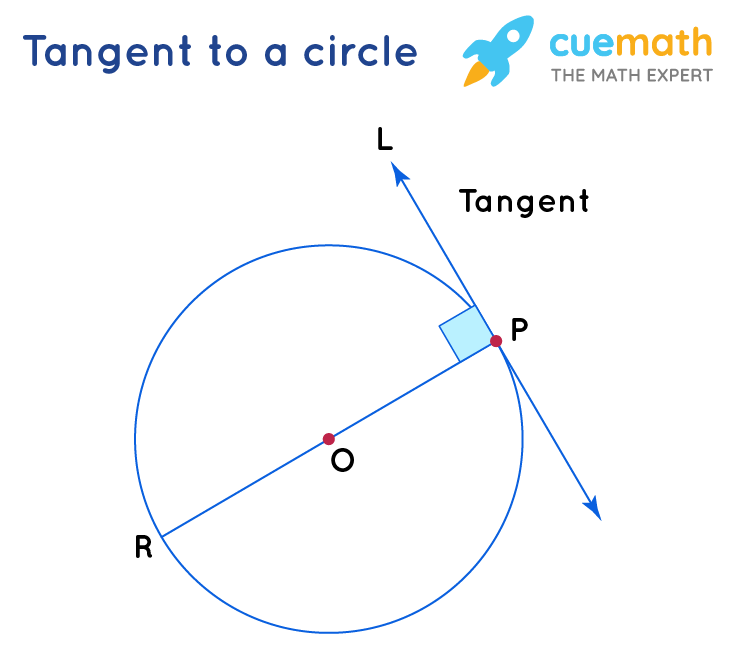
Tangent Circle Formula Learn The Formula Of Tangent Circle Along With In the given figure, there is one tangent and one secant. given that, pq = 5 cm, qr = 15 cm. therefore, pr = pq qr = (5 15) = 20 cm. now, according to the formula of the tangent of a circle, sr 2 = pr × qr. sr 2 = 20× 15 = 300 = 17.32 cm. find the length of the tangent pr if the radius of the given circle is 6 m. A tangent to a circle is a line which intersects the circle in exactly one point. in figure 1 line ab←→ a b ↔ is a tangent, intersecting circle o o just at point p p. figure 1. ab←→ a b ↔ is tangent to circle o o at point p p. a tangent has the following important property: theorem 7.3.1 7.3. 1. a tangent is perpendicular to the. A tangent to a circle is a straight line, in the plane of the circle, which touches the circle at only one point. the point is called the point of tangency or the point of contact. tangent to a circle theorem: a tangent to a circle is perpendicular to the radius drawn to the point of tangency. Example 1: standard diagram. points a, b, a,b, and c c are on the circumference of a circle with point o o as the center. ( (this can also be called circle o.) \, de o.)de is a tangent at point a. a. calculate the size of angle bad. b ad. locate the key parts of the circle for the theorem.
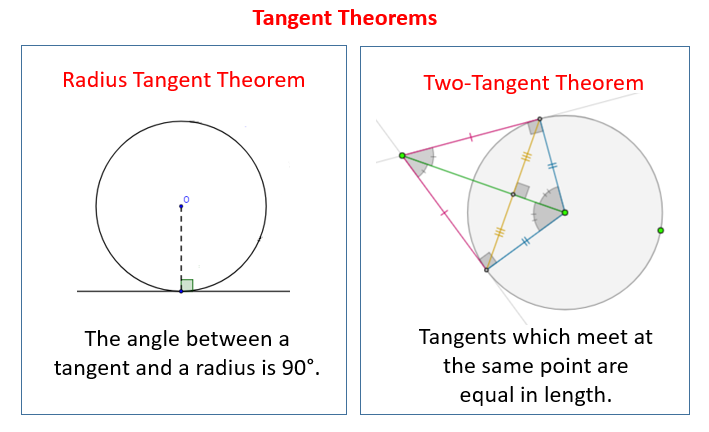
Tangents Of Circles A tangent to a circle is a straight line, in the plane of the circle, which touches the circle at only one point. the point is called the point of tangency or the point of contact. tangent to a circle theorem: a tangent to a circle is perpendicular to the radius drawn to the point of tangency. Example 1: standard diagram. points a, b, a,b, and c c are on the circumference of a circle with point o o as the center. ( (this can also be called circle o.) \, de o.)de is a tangent at point a. a. calculate the size of angle bad. b ad. locate the key parts of the circle for the theorem. Tangent is a line and to write the equation of a line we need two things, slope (m) and a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1. Knowing these essential theorems regarding circles and tangent lines, you are going to be able to identify key components of a circle, determine how many points of intersection, external tangents, and internal tangents two circles have, as well as find the value of segments given the radius and the tangent segment. video – lesson & examples.
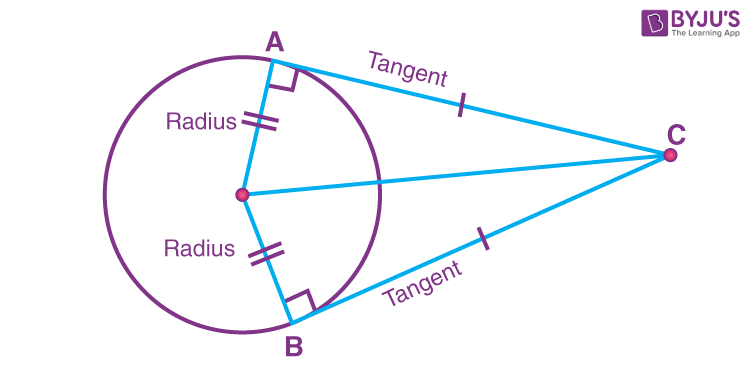
Tangent To A Circle Definition Equation Theorems Example Tangent is a line and to write the equation of a line we need two things, slope (m) and a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1. Knowing these essential theorems regarding circles and tangent lines, you are going to be able to identify key components of a circle, determine how many points of intersection, external tangents, and internal tangents two circles have, as well as find the value of segments given the radius and the tangent segment. video – lesson & examples.

Comments are closed.