Theorem The Lengths Of Tangents Drawn From An External Point To A

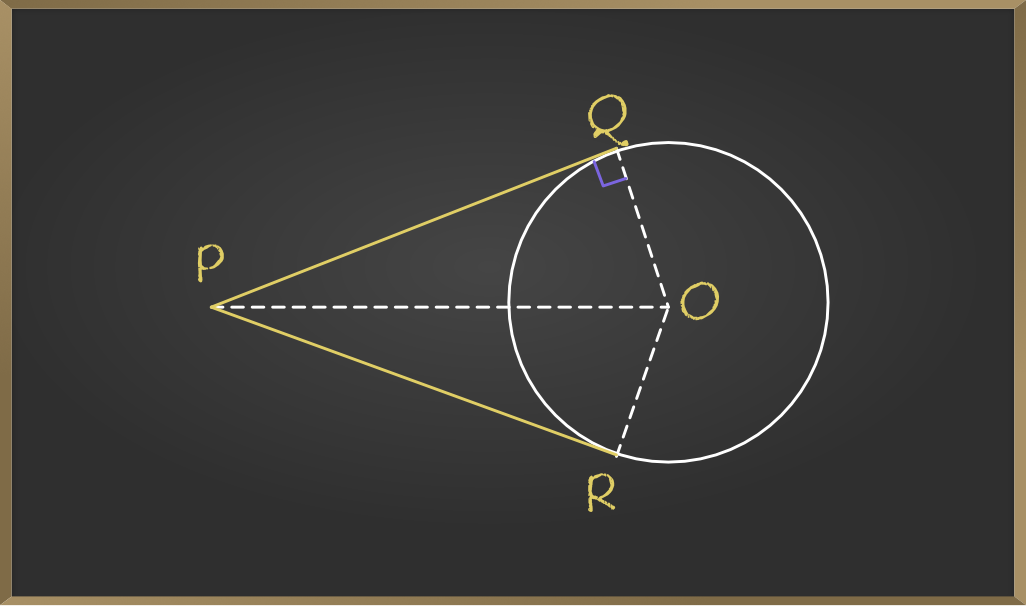
Theorem The Lengths Of Tangents Drawn From An External Point To A Transcript. theorem 10.2 (method 1) the lengths of tangents drawn from an external point to a circle are equal. given: let circle be with centre o and p be a point outside circle pq and pr are two tangents to circle intersecting at point q and r respectively to prove: lengths of tangents are equal i.e. pq = pr construction: join oq , or and op proof: as pq is a tangent oq ⊥ pq so, ∠ oqp. Solution. let ap and bp be the two tangents to the circle with centre o. to prove : ap = bp. proof : in Δ aop and Δ bop. oa = ob (radii of the same circle) ∠oap =∠obp = 90∘ (since tangent at any point of a circle is perpendicular to the radius through the point of contact) op = op (common) ∴ Δaop ≅Δbop (by r.h.s. congruence criterion).

Theorem 10 2 Class 10 Tangents From External Point Of Circle Are To prove: the lengths of tangents drawn from an external point to a circle are equal . let pq and pr be the two tangents drawn to the circle of centre o as shown in the figure. construction. draw a line segment, from centre o to external point p { i.e. p is the intersecting point of both the tangents} now ∆por and ∆poq. Theorem 10.2 : the lengths of tangents drawn from an external point to a circle are equal. proof : we are given a circle with centre o, a point p lying outside the circle and two tangents pq, pr on the circle from p (see fig. 10.7). we are required to prove that pq = pr. for this, we join op, oq and or. then ∠ oqp and ∠ orp are right angles. Theorem 2: two tangents theorem. the lengths of two tangents from a common external point to a circle are equal. the two tangents will subtend equal angles at the center. the line that connects the exterior point to the center will divide the angle between the tangents into two equal angles. The length of a tangent is equal to the length of a line segment with end points as the external point and the point of contact. so, \ (\begin {array} {l}pt {1}\end {array} \) and. \ (\begin {array} {l}pt {2}\end {array} \) are the lengths of tangent to the circle from an external point. \ (\begin {array} {l}p\end {array} \).

The Lengths Of Two Tangents Drawn From An External Point To A Circle Theorem 2: two tangents theorem. the lengths of two tangents from a common external point to a circle are equal. the two tangents will subtend equal angles at the center. the line that connects the exterior point to the center will divide the angle between the tangents into two equal angles. The length of a tangent is equal to the length of a line segment with end points as the external point and the point of contact. so, \ (\begin {array} {l}pt {1}\end {array} \) and. \ (\begin {array} {l}pt {2}\end {array} \) are the lengths of tangent to the circle from an external point. \ (\begin {array} {l}p\end {array} \). A tangent from p has been drawn to s. this is an example of a tangent from an external point: how many tangents do you think can be drawn from an external point to a circle? the answer is two, and the following theorem proves this fact. theorem: exactly two tangents can be drawn from an exterior point to a given circle. In this video, we have solved the theorem 10.2 : the lengths of tangents drawn from an external point to a circle are equal.subscribe to our channel.