Theorems Circle Euclidean Geometry

Circle Theorem Tips Euclidean Geometry Physics Mathematics Angle sum theorem (euclidean geometry form) the sum of the angles of a triangle is equal to two right angles. [so for an n gon, exactly 180(n − 2).] proof: consider any triangle, say abc. at a on ab, and on the opposite side, copy ∠abc, say ∠dab, and at a on ac, and on the opposite side, copy ∠acb to obtain ∠eac. Grade 11 euclidean geometry 2014 8 4.3 proof of theorems all seven theorems listed in the caps document must be proved. however, there are four theorems whose proofs are examinable (according to the examination guidelines 2014) in grade 12. in this guide, only four examinable theorems are proved. these four theorems are written in bold. 1.

Circle Theorems Wksheet Elementary Geometry Euclidean Plane Geometry Accessed 4 november 2024. euclidean geometry is the study of plane and solid figures on the basis of axioms and theorems employed by the ancient greek mathematician euclid. the term refers to the plane and solid geometry commonly taught in secondary school. euclidean geometry is the most typical expression of general mathematical thinking. Euclidean geometry is a mathematical system attributed to ancient greek mathematician euclid, which he described in his textbook on geometry, elements. euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. although many of euclid's results had. 8.2 circle geometry (embj9) the following terms are regularly used when referring to circles: arc — a portion of the circumference of a circle. chord — a straight line joining the ends of an arc. circumference — the perimeter or boundary line of a circle. radius (\ (r\)) — any straight line from the centre of the circle to a point on. Euclid's postulates. 1. a straight line segment can be drawn joining any two points. 2. any straight line segment can be extended indefinitely in a straight line. 3. given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. 4. all right angles are congruent.

Euclidean Circle Geometry Theorem 5 Youtube 8.2 circle geometry (embj9) the following terms are regularly used when referring to circles: arc — a portion of the circumference of a circle. chord — a straight line joining the ends of an arc. circumference — the perimeter or boundary line of a circle. radius (\ (r\)) — any straight line from the centre of the circle to a point on. Euclid's postulates. 1. a straight line segment can be drawn joining any two points. 2. any straight line segment can be extended indefinitely in a straight line. 3. given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. 4. all right angles are congruent. Example 5: chord of a circle (cosine ratio) below is a circle with centre c. points a, b, c, and d are on the circumference of the circle. the chord ab is perpendicular to the line cd at the point e. the line ae is 5cm 5cm and angle ade =71o = 71o. calculate the length of the line bc correct to 1 1 decimal place. Challenge problems. \ (bc\) is tangent to both a circle with center at \ (a\) and a circle with center at \ (d\). the area of the circle with center at \ (a\) is \ (225\pi\) and the area of the circle with center at \ (d\) is \ (36\pi\). if \ (bc=16\), find the distance between the centers of the two circles.
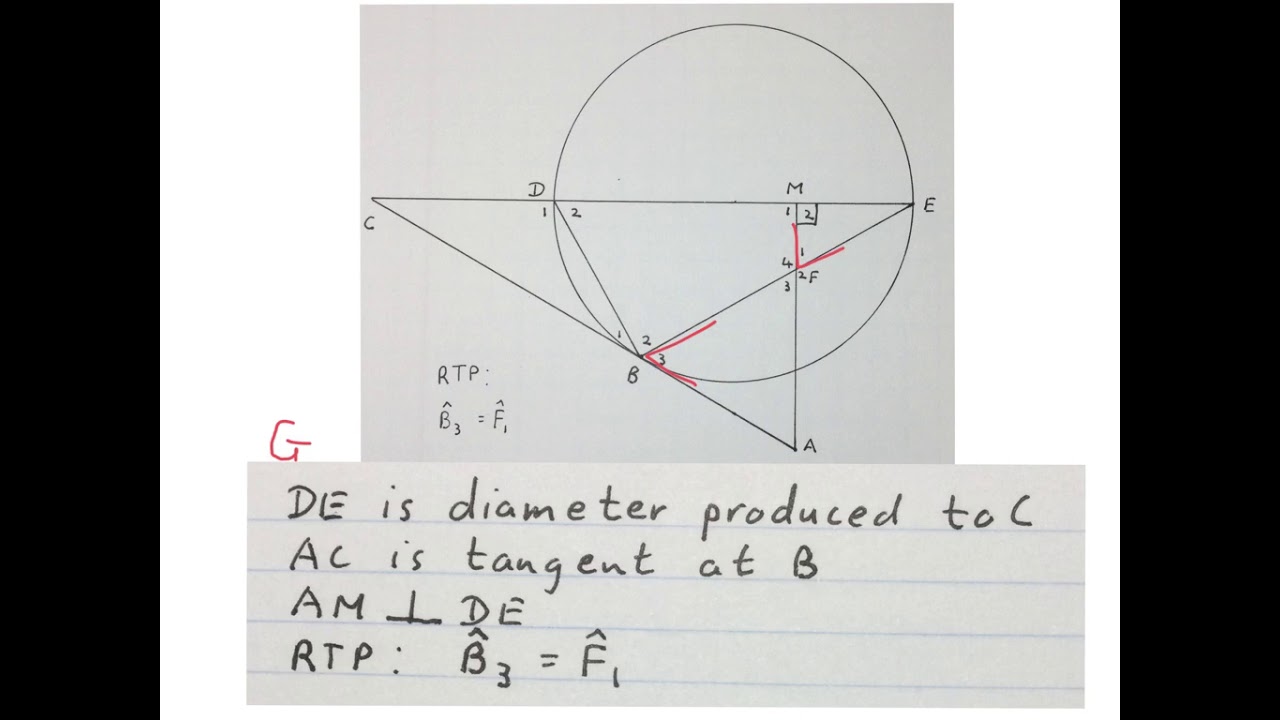
Euclidean Geometry Circle Theorem Riders 11 20 Mathdou Grade 11 And Example 5: chord of a circle (cosine ratio) below is a circle with centre c. points a, b, c, and d are on the circumference of the circle. the chord ab is perpendicular to the line cd at the point e. the line ae is 5cm 5cm and angle ade =71o = 71o. calculate the length of the line bc correct to 1 1 decimal place. Challenge problems. \ (bc\) is tangent to both a circle with center at \ (a\) and a circle with center at \ (d\). the area of the circle with center at \ (a\) is \ (225\pi\) and the area of the circle with center at \ (d\) is \ (36\pi\). if \ (bc=16\), find the distance between the centers of the two circles.

Euclidean Geometry Rules Maths At Sharp
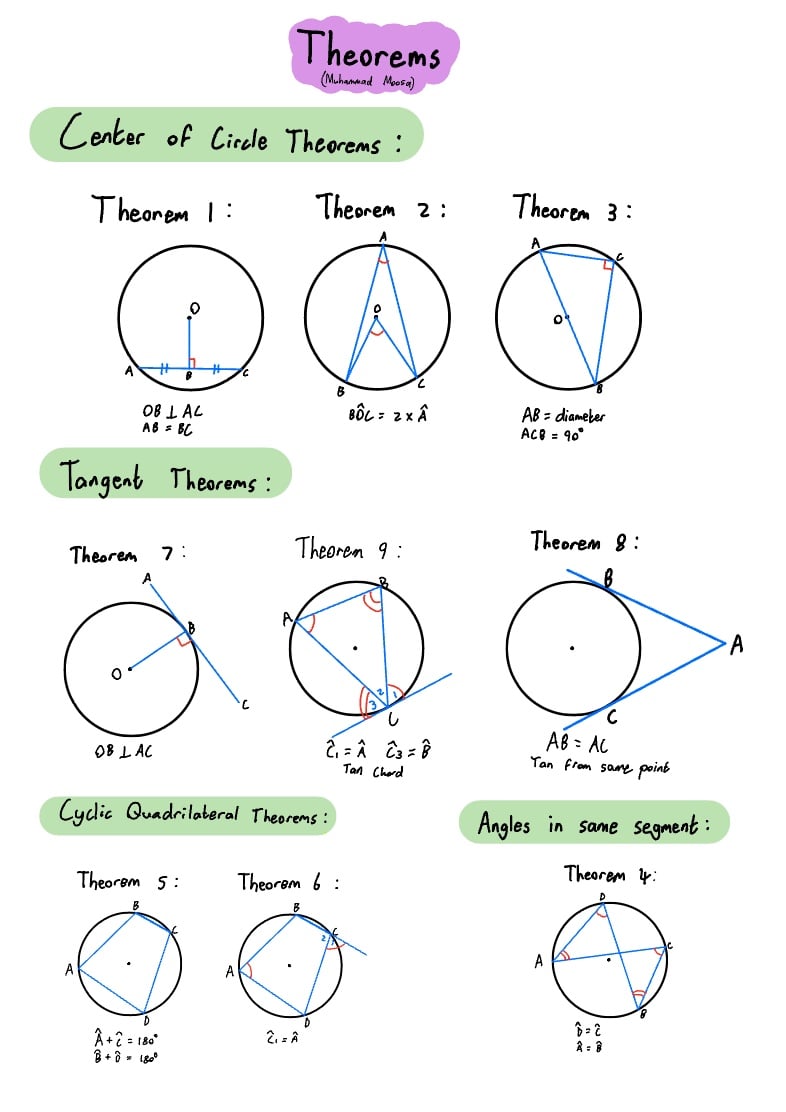
Euclidean Geometry Theorems Notability Gallery

Comments are closed.