Three Circles Tangent To Each Other See Figure Have Their Centres On T

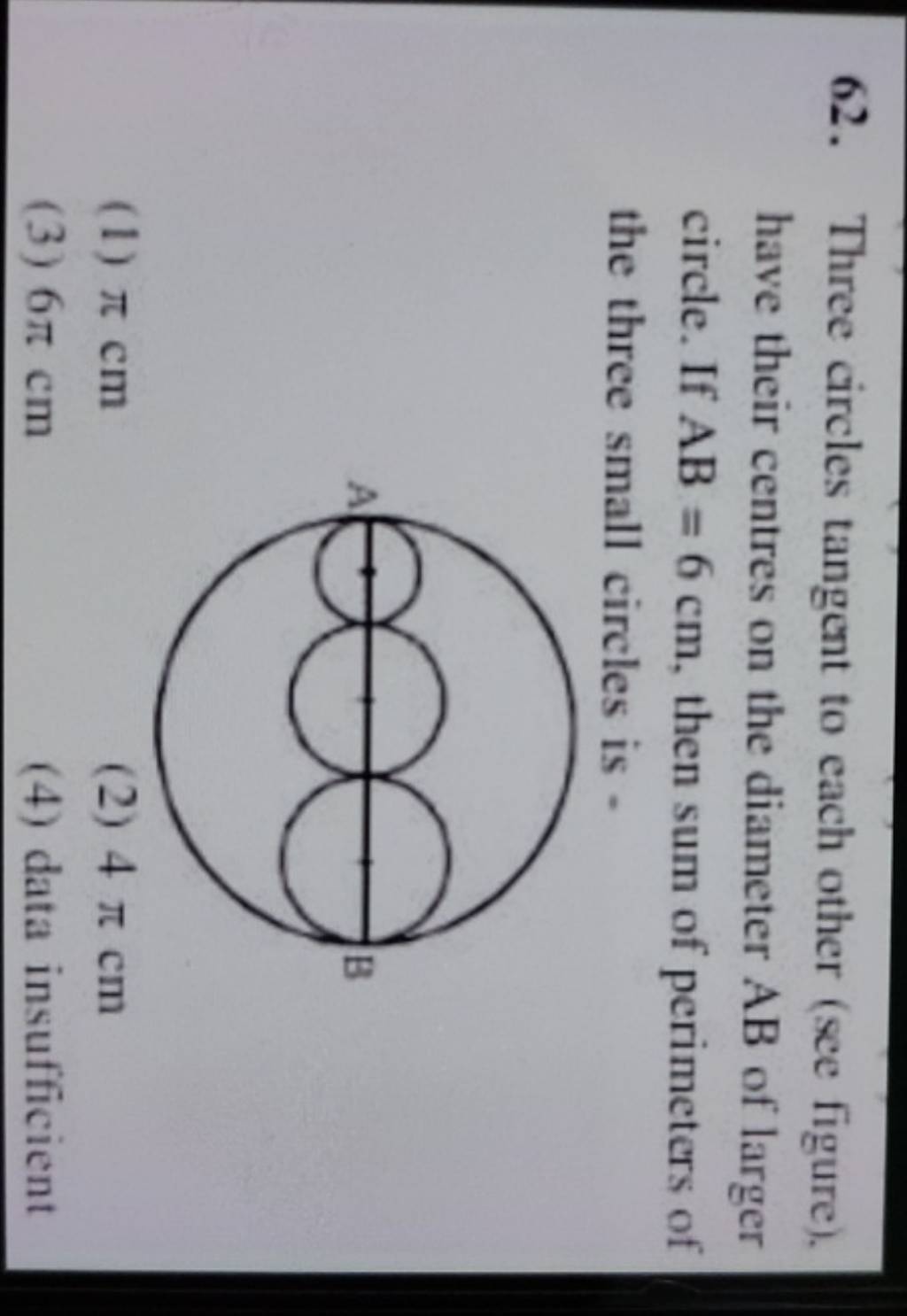
Three Circles Tangent To Each Other See Figure Have Their Centres On T Three circles with radii 1, 2, and 3 ft. are externally tangent to one another, as shown in the figure. find the area of the sector of the circle of radius 1 ft. that is cut off by the line segments joining the center of that circle to the centers of the other two circles. the length of the sides of a triangle is calculated by the sum of the. Solution 1. let be the center of circle for all and let be the tangent point of . since the radius of is the diameter of , the radius of is . let the radius of be and let . if we connect , we get an isosceles triangle with lengths . then right triangle has legs and hypotenuse . solving for , we get . also, right triangle has legs , and hypotenuse .

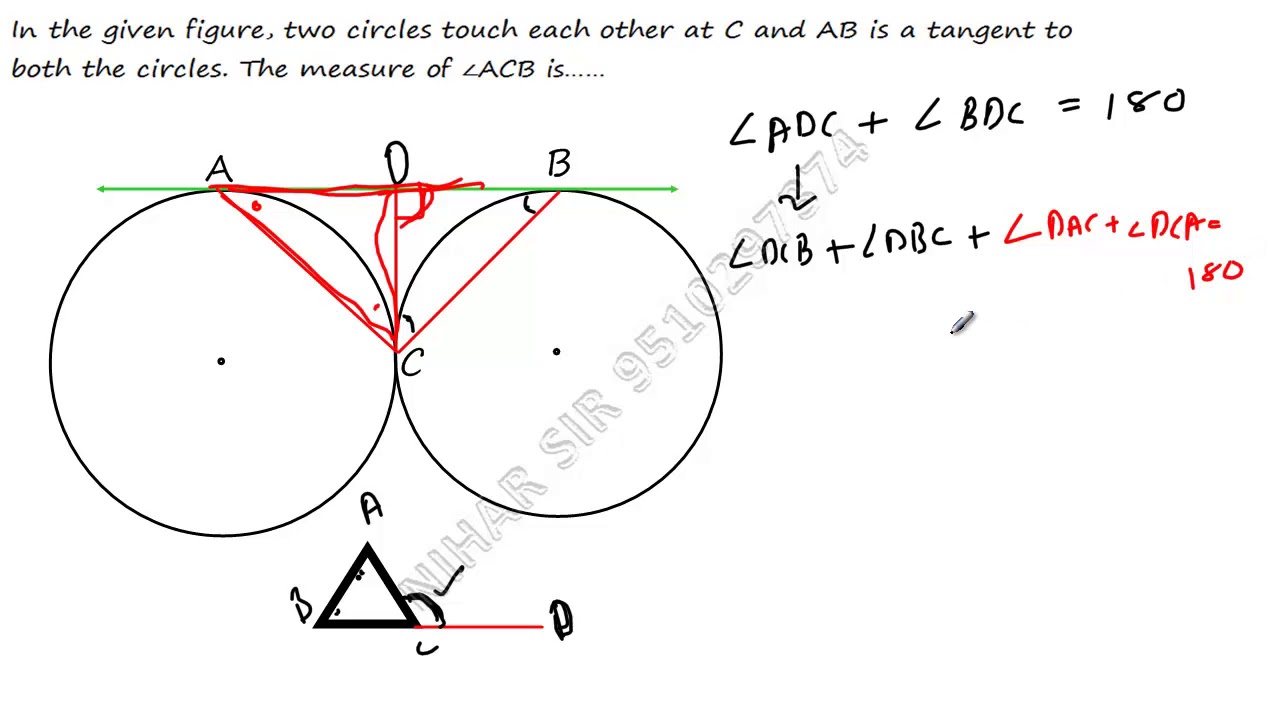
Three Circles Tangent To Each Other Now let three circles be drawn, one centered about each point and each one tangent to the other two (left figure), and call the radii, , . interestingly, the pairwise external similitude centers of these circles are the three nobbs points (p. moses, pers. comm., mar. 14, 2005). 0. if the radius of the circle is 1, the radius of three circles that will be internally tangent is 2 3–√ − 3 ≈ 0.464 2 3 − 3 ≈ 0.464 by soddy's formula, given in the soddy's circles section of this. you can construct this length, then mark it off on a diameter of the circle to find one of the centers, and finish constructing the. The radius of circle a is equal to 10 cm and the radius of circle b is equal to 8 cm. find the radius of circle c. solution to problem. let a, b and c be the radii of the three circles. we first draw the lines aa', bb' and cc' perpendicular to line l. b'c, ca' and ba" are parallel to line l. let x = b'c, y=a'c and z = ba". Tangencies: three tangent circles. any three points can be the centers of three mutually tangent circles. to construct the circles, form a triangle from the three centers, bisect its angles (blue), and drop perpendiculars from the point where the bisectors meet to the three sides (green). the points where these perpendiculars cross the sides.

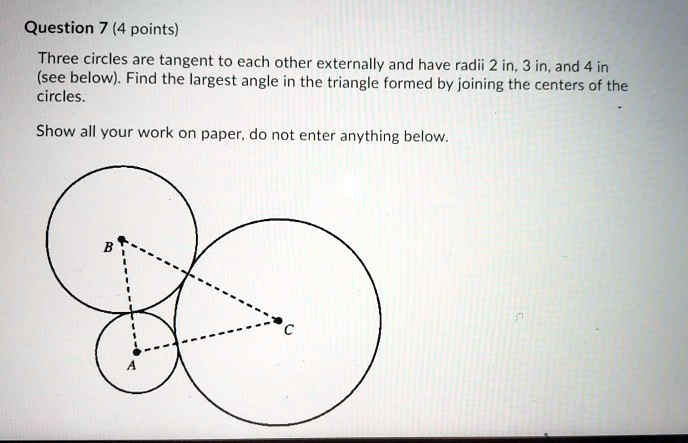
Question 7 4 Points Three Circles Are Tangent To Each Other The radius of circle a is equal to 10 cm and the radius of circle b is equal to 8 cm. find the radius of circle c. solution to problem. let a, b and c be the radii of the three circles. we first draw the lines aa', bb' and cc' perpendicular to line l. b'c, ca' and ba" are parallel to line l. let x = b'c, y=a'c and z = ba". Tangencies: three tangent circles. any three points can be the centers of three mutually tangent circles. to construct the circles, form a triangle from the three centers, bisect its angles (blue), and drop perpendiculars from the point where the bisectors meet to the three sides (green). the points where these perpendiculars cross the sides. Given a circle, construct three circles tangent to it and tangent to each other. surprisingly, i can find no reference to this (although there are many similar sounding problems, and apollonius' problem, none of which solve this.) my solution is below. i request verification, improvements to the exposition, or alternate solutions. Diagram shows three circles, each of radius 1cm, centres a, b, and c. each circle touches the other two. from here you can get the area of triangle abc:.

910 Ge Three Circles Tangent To Each Other Youtube Given a circle, construct three circles tangent to it and tangent to each other. surprisingly, i can find no reference to this (although there are many similar sounding problems, and apollonius' problem, none of which solve this.) my solution is below. i request verification, improvements to the exposition, or alternate solutions. Diagram shows three circles, each of radius 1cm, centres a, b, and c. each circle touches the other two. from here you can get the area of triangle abc:.

Apollonius Problem For Three Mutually Tangent Circles The Centres Are