Three Tangent Circles

Math Principles Three Tangent Circles Tangent circles. download wolfram notebook. two circles with centers at with radii for are mutually tangent if. (1) if the center of the second circle is inside the first, then the and signs both correspond to internally tangent circles. if the center of the second circle is outside the first, then the sign corresponds to externally tangent. Malfatti's problem is to carve three cylinders from a triangular block of marble, using as much of the marble as possible. in 1803, gian francesco malfatti conjectured that the solution would be obtained by inscribing three mutually tangent circles into the triangle (a problem that had previously been considered by japanese mathematician ajima naonobu); these circles are now known as the.

Math Principles Three Tangent Circles Tangencies: three tangent circles. any three points can be the centers of three mutually tangent circles. to construct the circles, form a triangle from the three centers, bisect its angles (blue), and drop perpendiculars from the point where the bisectors meet to the three sides (green). the points where these perpendiculars cross the sides. Three circles with radii 1, 2, and 3 ft. are externally tangent to one another, as shown in the figure. find the area of the sector of the circle of radius 1 ft. that is cut off by the line segments joining the center of that circle to the centers of the other two circles. the length of the sides of a triangle is calculated by the sum of the. The radius of circle a is equal to 10 cm and the radius of circle b is equal to 8 cm. find the radius of circle c. solution to problem. let a, b and c be the radii of the three circles. we first draw the lines aa', bb' and cc' perpendicular to line l. b'c, ca' and ba" are parallel to line l. let x = b'c, y=a'c and z = ba". 0. if the radius of the circle is 1, the radius of three circles that will be internally tangent is 2 3–√ − 3 ≈ 0.464 2 3 − 3 ≈ 0.464 by soddy's formula, given in the soddy's circles section of this. you can construct this length, then mark it off on a diameter of the circle to find one of the centers, and finish constructing the.
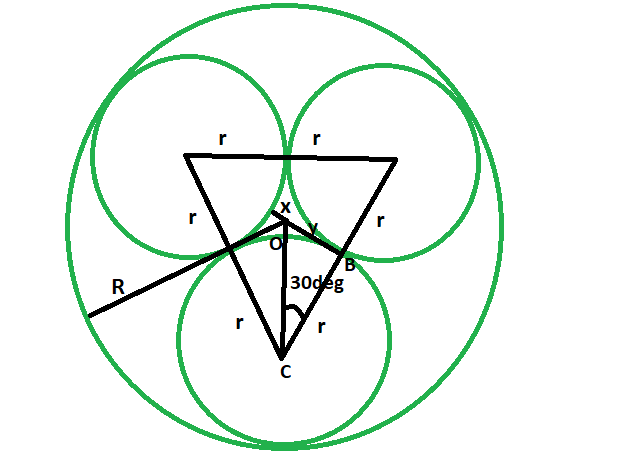
Radii Of The Three Tangent Circles Of Equal Radius Which Are Inscribed The radius of circle a is equal to 10 cm and the radius of circle b is equal to 8 cm. find the radius of circle c. solution to problem. let a, b and c be the radii of the three circles. we first draw the lines aa', bb' and cc' perpendicular to line l. b'c, ca' and ba" are parallel to line l. let x = b'c, y=a'c and z = ba". 0. if the radius of the circle is 1, the radius of three circles that will be internally tangent is 2 3–√ − 3 ≈ 0.464 2 3 − 3 ≈ 0.464 by soddy's formula, given in the soddy's circles section of this. you can construct this length, then mark it off on a diameter of the circle to find one of the centers, and finish constructing the. Given three noncollinear points, construct three tangent circles such that one is centered at each point and the circles are pairwise tangent to one another. then there exist exactly two nonintersecting circles that are tangent to all three circles. these are called the inner and outer soddy circles, and their centers are called the inner s and outer soddy centers s^', respectively. frederick. Tangent lines to circles. in euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs.

Comments are closed.