Three Tangent Circles Problem Find Radius Of The Red Circle Gradient
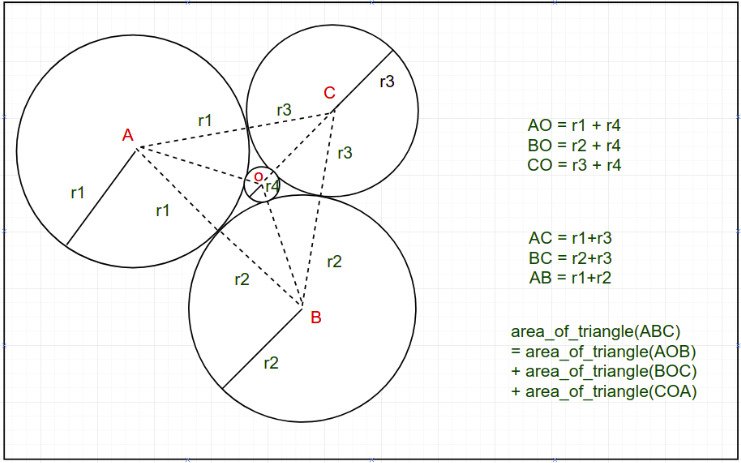
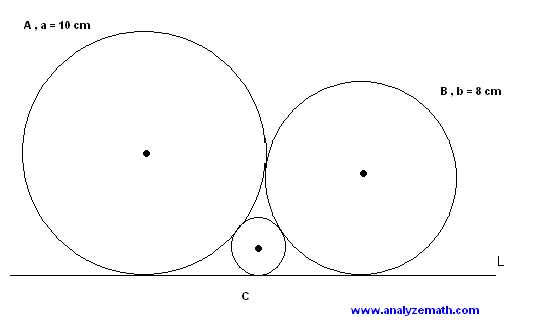
Radius Of The Inscribed Circle Within Three Tangent Circles Geeksforgeeks Three tangent circles problem find radius of the red circle | gradientwe will find a solution to classic problem of three tangent circles, and make the for. The radius of circle a is equal to 10 cm and the radius of circle b is equal to 8 cm. find the radius of circle c. solution to problem. let a, b and c be the radii of the three circles. we first draw the lines aa', bb' and cc' perpendicular to line l. b'c, ca' and ba" are parallel to line l. let x = b'c, y=a'c and z = ba".
Three Tangent Circles Problem With Solution How can i find the equation of the tangent line to a circle at a given point? step 1: find the gradient of the radius op. step 2: find the gradient of the tangent. step 3: the equation of the tangent is the equation of the line with that gradient that goes through point p (see equation of a straight line). Tangencies: three tangent circles. any three points can be the centers of three mutually tangent circles. to construct the circles, form a triangle from the three centers, bisect its angles (blue), and drop perpendiculars from the point where the bisectors meet to the three sides (green). the points where these perpendiculars cross the sides. 0. if the radius of the circle is 1, the radius of three circles that will be internally tangent is 2 3–√ − 3 ≈ 0.464 2 3 − 3 ≈ 0.464 by soddy's formula, given in the soddy's circles section of this. you can construct this length, then mark it off on a diameter of the circle to find one of the centers, and finish constructing the. Created with geogebra. three circles (o), with centers at o, i = 1, 2, 3, touch pairwise externally. if i, j, k are three different indices obtained from 1, 2, 3 by a cyclic permutation, then p k denotes the point of contact of (o) and (o). p p extended crosses again (o) in q k and (o) in r k. the circle (a k) tangent to (o) in q k and (o) in r.
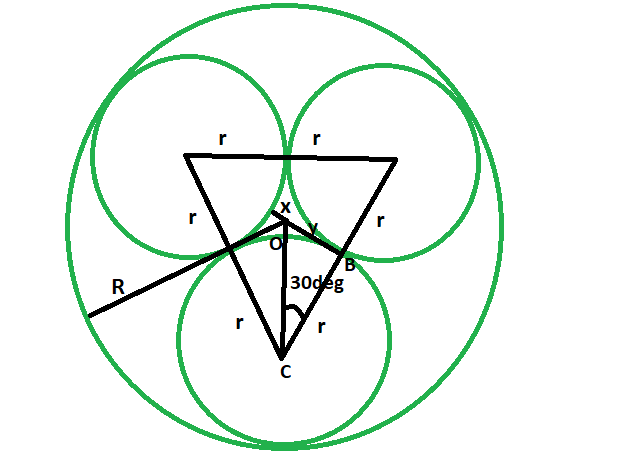
Radii Of The Three Tangent Circles Of Equal Radius Which Are Inscribed 0. if the radius of the circle is 1, the radius of three circles that will be internally tangent is 2 3–√ − 3 ≈ 0.464 2 3 − 3 ≈ 0.464 by soddy's formula, given in the soddy's circles section of this. you can construct this length, then mark it off on a diameter of the circle to find one of the centers, and finish constructing the. Created with geogebra. three circles (o), with centers at o, i = 1, 2, 3, touch pairwise externally. if i, j, k are three different indices obtained from 1, 2, 3 by a cyclic permutation, then p k denotes the point of contact of (o) and (o). p p extended crosses again (o) in q k and (o) in r k. the circle (a k) tangent to (o) in q k and (o) in r. Given three lines, find a tangent circle: this is like finding the incircle of a triangle. pick two lines, construct an angle bisecting line. pick another pair of the original lines, construct another angle bisecting line. the intersection of the bisecting lines gives the center of the circle. the rest is left to you. According to wolframalpha's page on tangent circles, the radius of c3 c 3 can be calculated using the following formula r3 = r1×r2 (r1√ r2√)2 r 3 = r 1 × r 2 (r 1 r 2) 2, which can be simplified to 1 r3√ = 1 r1√ 1 r2√ 1 r 3 = 1 r 1 1 r 2. to be completely honest, i'm having a hard time understanding understanding how this.

3 Tangent Circles Red Area R Geometry Given three lines, find a tangent circle: this is like finding the incircle of a triangle. pick two lines, construct an angle bisecting line. pick another pair of the original lines, construct another angle bisecting line. the intersection of the bisecting lines gives the center of the circle. the rest is left to you. According to wolframalpha's page on tangent circles, the radius of c3 c 3 can be calculated using the following formula r3 = r1×r2 (r1√ r2√)2 r 3 = r 1 × r 2 (r 1 r 2) 2, which can be simplified to 1 r3√ = 1 r1√ 1 r2√ 1 r 3 = 1 r 1 1 r 2. to be completely honest, i'm having a hard time understanding understanding how this.
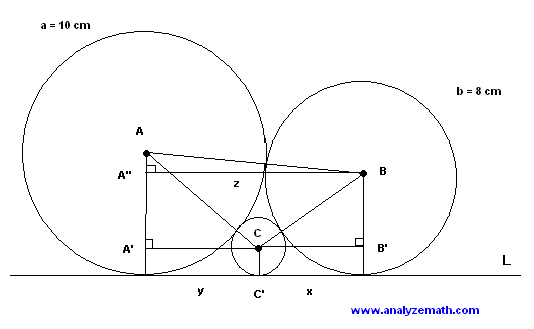
Three Tangent Circles Problem With Solution

Soddy Circles And Descartes Theorem Three Tangent Circles Ipad Apps

Comments are closed.