Three Tangent Circles Sangaku
Three Tangent Circles Sangaku Three tangent circles sangaku. this is one of the rather more popular on the web sangaku problems: given three circles tangent to each other and to a straight line, express the radius of the middle circle via the radii of the other two. (see [fukagawa & pedoe, 1.1.2] where it is mentioned that the tablet survives in the miyagai prefecture and. This is japanese temple problem (sangaku problem) in which three circles are tangent to each other.follow me: twitter sybermathclick!!!:.

Three Tangent Circles Sangaku Sangaku geometry theorem: three circles and a tangent line. in the figure below, three circles of radiii: a, b, c are mutually tangent to each other and a line. prove that: . references: fukagawa hidetoshi, tony rothman, "sacred mathematics: japanese temple geometry" (princenton university press, 2008). see also: geometry problem 1154. Sangaku (算額, lit. "calculation tablet") are japanese geometry problems presented on wooden tablets. these tablets were hung in buddhist temples and shinto shrines during the edo period (1603 1867) in the 18th to 19th centuries. the following sangaku problem is from a tablet in gunma prefecture that dates to 1824. there are three mutually tangent circles resting on a line. find the radius. Sangaku with versines. sangakus with a mixtilinear circle. sequences of touching circles. square and circle in a gothic cupola. steiner's sangaku. tangent circles and an isosceles triangle. the squinting eyes theorem. three incircles in a right triangle. three squares and two ellipses. Sangaku are often colorful tablets offered in shinto shrines (and sometimes in buddhist temples) in japan and posing mathematical problems. the earliest sangaku date a few years before the beginning of the japanese edo period (1603 1867) of self imposed seclusion from the western world. most of the write ups on the sangaku phenomenon are based.
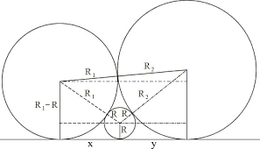
Sangaku Three Tangent Circles Problem Math Physics Problems Wikia Sangaku with versines. sangakus with a mixtilinear circle. sequences of touching circles. square and circle in a gothic cupola. steiner's sangaku. tangent circles and an isosceles triangle. the squinting eyes theorem. three incircles in a right triangle. three squares and two ellipses. Sangaku are often colorful tablets offered in shinto shrines (and sometimes in buddhist temples) in japan and posing mathematical problems. the earliest sangaku date a few years before the beginning of the japanese edo period (1603 1867) of self imposed seclusion from the western world. most of the write ups on the sangaku phenomenon are based. The ratio of radiuses of two big circle is: ¯ ol ¯ oc = 2√7cos (arccos (√7 14) 3) − 1 3 ≈ 1.246979603717467. if we take the radius of the smaller circle ¯ bj = 1 then the radiuses of two big circles are: ¯ ol ≈ 3.603875471609681, ¯ oc ≈ 2.890083735825261. i used inversion with the center of o, the blue circle as inversion. Geometric art: sangaku problem: three circles and a tangent line: in the figure below, three circles of radiii: a, b, c are mutually tangent to each other and a line. prove that: . see also: original sangaku japanese problem.

Comments are closed.