Vectores En El Espacio Producto Punto Interpretacion Geometrica

Vectores En El Espacio Producto Punto Interpretacion Geometrica Fórmulas de vectores; teorÍa. vectores en el espacio; operaciones de vectores; vectores paralelos y vector normal. base de vectores; combinación lineal; producto escalar; aplicaciones del producto escalar; problemas. problemas de vectores en el espacio. problemas de producto escalar. problemas de producto vectorial y producto mixto. El producto punto es uno de los conceptos fundamentales en el estudio de la geometría analítica y el álgebra lineal. este producto, también conocido como «producto escalar», permite establecer una relación numérica entre dos vectores en un espacio euclidiano, proporcionando una herramienta valiosa para analizar propiedades como la longitud, el ángulo y la ortogonalidad entre ellos.

13 Interpretación Geométrica Del Producto Escalar Cálculo De La 2.1. vectores fijos y vectores libres (en el plano y en el espacio) el vector que tiene por origen el punto a y por extremo el punto b, se llama vector fijo ab. − módulo del vector es la longitud del segmento ab. se denota ab. − dirección de es la de la recta que contiene a a y a b. − sentido de es el que indica el traslado de a a b. La ecuación estándar de una esfera con centro (a, b, c) y radio r es (x − a)2 (y − b)2 (z − c)2 = r2. en tres dimensiones, como en dos, los vectores se expresan comúnmente en forma de componentes ⇀ v = x, y, z , o en términos de los vectores unitarios estándar, ⇀ v = xˆi yˆj z ˆk. El producto punto podemos definir un producto interior de vectores en el espacio de manera similar a como se hizo en el plano. si u = (u1,u2,u3) y v = (v1,v2,v3) el producto punto (o producto interno o producto escalar) de u y v es el número u ∙ v = u 1 v 1 u 2 v 2 u 3 v 3 ejemplo. el producto punto de los vectores u=(1,2,3) y v=(4,5, 6) es. Interpretación geométrica del producto escalar. el producto de dos vectores no nulos es igual al módulo de uno de ellos por la proyección del otro sobre él. en el dibujo, o a ′ es la proyección del vector u → sobre v →. si nos fijamos en el triángulo o a a ′ y aplicamos la fórmula del coseno, obtenemos:.

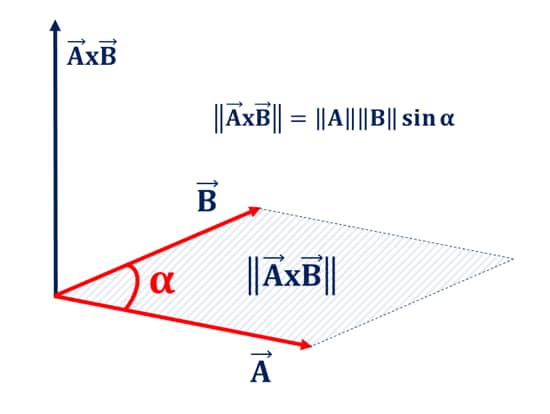
Producto Vectorial O Cruz De Vectores En Física El producto punto podemos definir un producto interior de vectores en el espacio de manera similar a como se hizo en el plano. si u = (u1,u2,u3) y v = (v1,v2,v3) el producto punto (o producto interno o producto escalar) de u y v es el número u ∙ v = u 1 v 1 u 2 v 2 u 3 v 3 ejemplo. el producto punto de los vectores u=(1,2,3) y v=(4,5, 6) es. Interpretación geométrica del producto escalar. el producto de dos vectores no nulos es igual al módulo de uno de ellos por la proyección del otro sobre él. en el dibujo, o a ′ es la proyección del vector u → sobre v →. si nos fijamos en el triángulo o a a ′ y aplicamos la fórmula del coseno, obtenemos:. Apuntes escolar matemáticas geometría analítica vectores interpretacion geometrica del producto escalar. el producto escalar de dos vectores no nulos es igual al módulo de uno de ellos por la proyección del otro sobre él. esto se obtiene de. 1 calcular el coseno del ángulo. 2 despejamos el cual es la proyección escalar de sobre el vector. El producto punto esencialmente nos dice cuánto del vector de fuerza se aplica en la dirección del vector de movimiento. el producto punto también puede ayudarnos a medir el ángulo formado por un par de vectores y la posición de un vector con respecto a los ejes de coordenadas. 12.3e: ejercicios para la sección 12.3; 12.4: el producto cruzado.

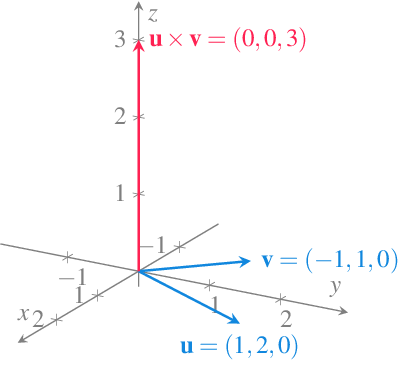
Manual De Análisis Matemático Real 10 Geometría Vectorial Del Plano Y Apuntes escolar matemáticas geometría analítica vectores interpretacion geometrica del producto escalar. el producto escalar de dos vectores no nulos es igual al módulo de uno de ellos por la proyección del otro sobre él. esto se obtiene de. 1 calcular el coseno del ángulo. 2 despejamos el cual es la proyección escalar de sobre el vector. El producto punto esencialmente nos dice cuánto del vector de fuerza se aplica en la dirección del vector de movimiento. el producto punto también puede ayudarnos a medir el ángulo formado por un par de vectores y la posición de un vector con respecto a los ejes de coordenadas. 12.3e: ejercicios para la sección 12.3; 12.4: el producto cruzado.