What Is A Cauchy Sequence вђ Cs Comics
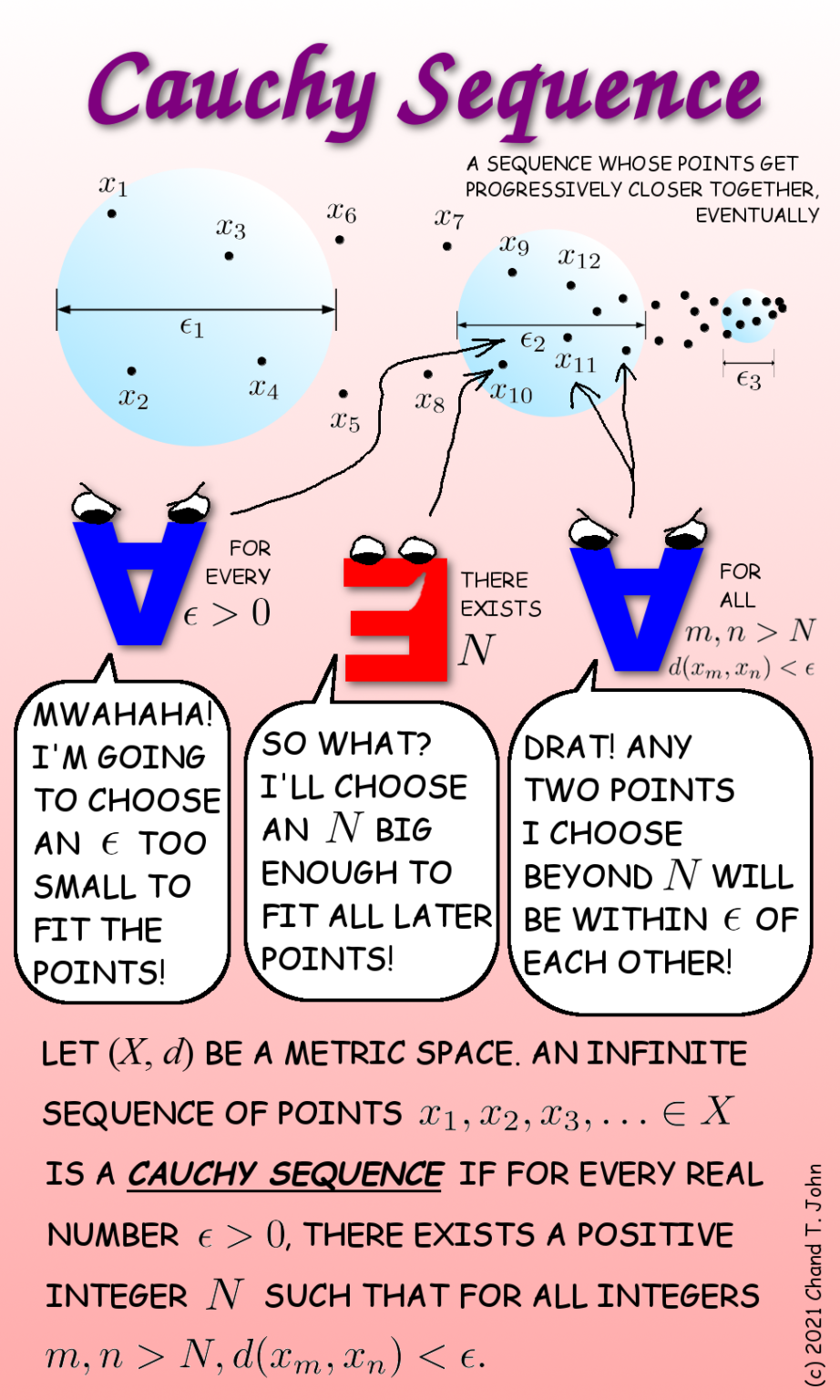
What Is A Cauchy Sequence Cs Comics Cs comics ‹ prev next › what is a cauchy sequence? by cscomics etvvcs on october 30, 2021 at 6:53 pm. posted in: uncategorized. sources: m. f. barnsley. 34. my question is related with the definition of cauchy sequence. as we know that a sequence (xn) (x n) of real numbers is called cauchy, if for every positive real number ε, there is a positive integer n ∈n n ∈ n such that for all natural numbers m, n> n m, n> n. ∣xm −xn ∣<ϵ ∣ x m − x n ∣<ϵ. my questions are.
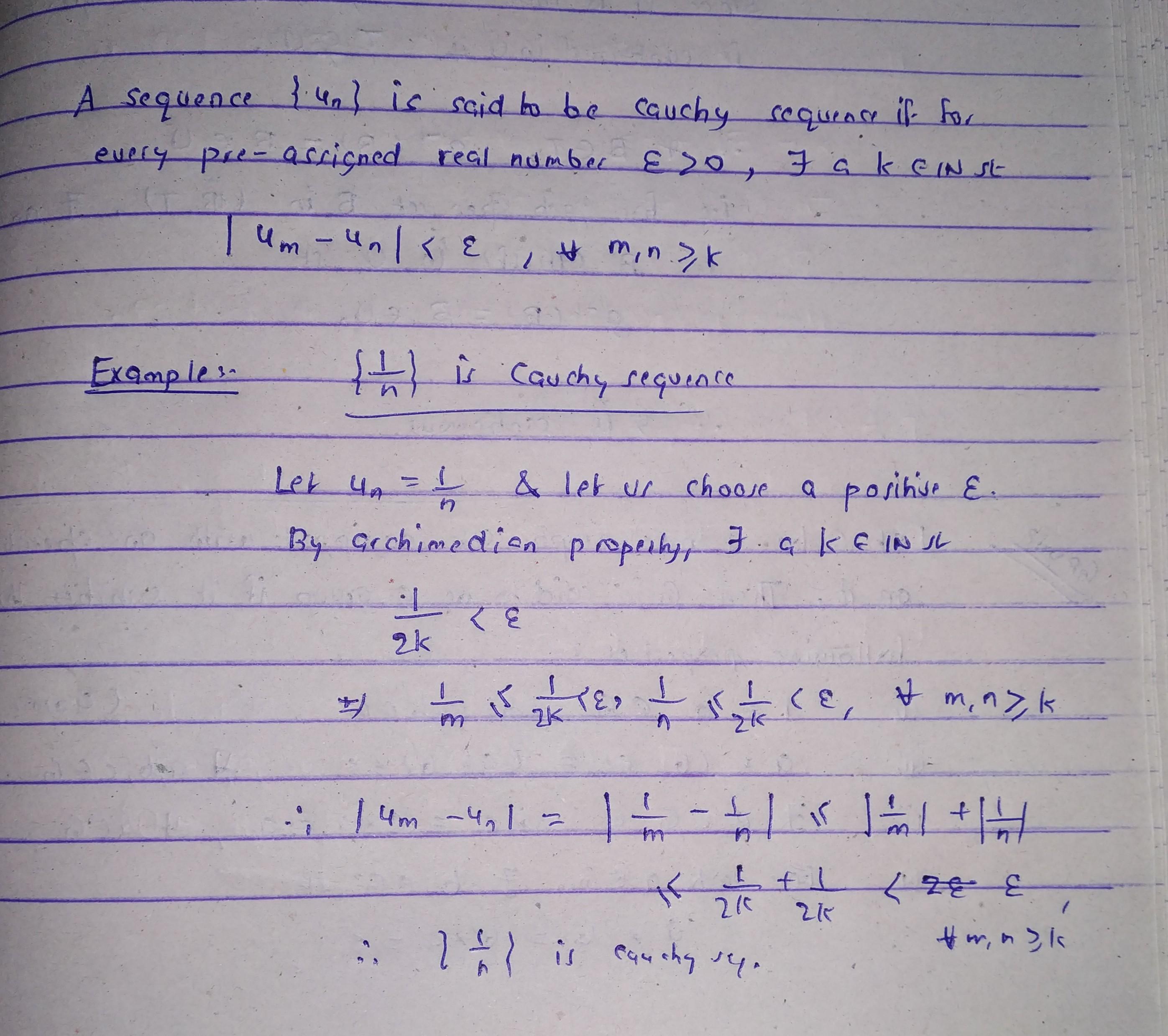
What Is The Definition Of Cauchy Sequence With An Example In mathematics, a cauchy sequence is a sequence whose elements become arbitrarily close to each other as the sequence progresses. [1] more precisely, given any small positive distance, all excluding a finite number of elements of the sequence are less than that given distance from each other. cauchy sequences are named after augustin louis. Cauchy sequences are useful because they give rise to the notion of a complete field, which is a field in which every cauchy sequence converges. because the cauchy sequences are the sequences whose terms grow close together, the fields where all cauchy sequences converge are the fields that are not ``missing" any numbers. A real sequence is called a cauchy sequence, if the following condition holds. for every , there exists an , such that for all , the estimate. holds. category: mathematical definition. not logged in. talk. contributions. create account. Definition 1. a sequence {an} is said to be cauchy (or to be a cauchy sequence) if for every real number 0, there is an integer n (possibly depending on ) for which. theorem 2. a sequence of real numbers is convergent if and only if it is cauchy. proof. (⇒) let {an} be a convergent sequence with limit l.

What Is The Definition Of Cauchy Sequence With An Example A real sequence is called a cauchy sequence, if the following condition holds. for every , there exists an , such that for all , the estimate. holds. category: mathematical definition. not logged in. talk. contributions. create account. Definition 1. a sequence {an} is said to be cauchy (or to be a cauchy sequence) if for every real number 0, there is an integer n (possibly depending on ) for which. theorem 2. a sequence of real numbers is convergent if and only if it is cauchy. proof. (⇒) let {an} be a convergent sequence with limit l. A cauchy sequence is an infinite sequence which ought to converge in the sense that successive terms get arbitrarily close together, as they would if they were getting arbitrarily close to a limit. among sequences, only cauchy sequences will converge; in a complete space, all cauchy sequence converge. In other words, a cauchy sequence is a sequence that gets arbitrarily close to some value, while a convergent sequence is a cauchy sequence that reaches that value. applications of cauchy sequences cauchy sequences have excellent properties that we have discussed above, so they can be used to understand and analyze the behavior of a system as.

Solved 2 Define What Is Meant By A Cauchy Sequence And Chegg A cauchy sequence is an infinite sequence which ought to converge in the sense that successive terms get arbitrarily close together, as they would if they were getting arbitrarily close to a limit. among sequences, only cauchy sequences will converge; in a complete space, all cauchy sequence converge. In other words, a cauchy sequence is a sequence that gets arbitrarily close to some value, while a convergent sequence is a cauchy sequence that reaches that value. applications of cauchy sequences cauchy sequences have excellent properties that we have discussed above, so they can be used to understand and analyze the behavior of a system as.

Comments are closed.